Geometry Formulas Reference

Shape	Formula
Input: Sides Lengths of Right Triangle	Pythagorean Theorem Formula $c^2 = a^2 + b^2$
Input: Two points $A(x_A,y_A)$ and $B(x_B,y_B)$	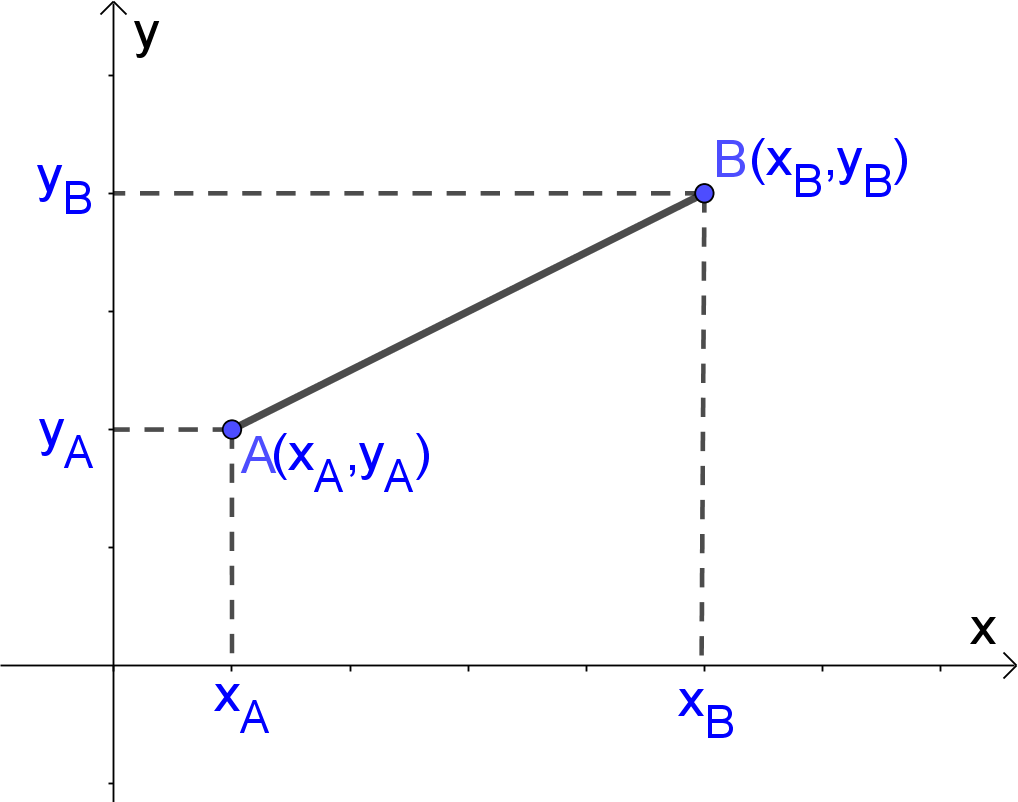Length Between Two Points ${AB}=d(A,B)=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
Input: Two points $A(x_A,y_A)$ and $B(x_B,y_B)$	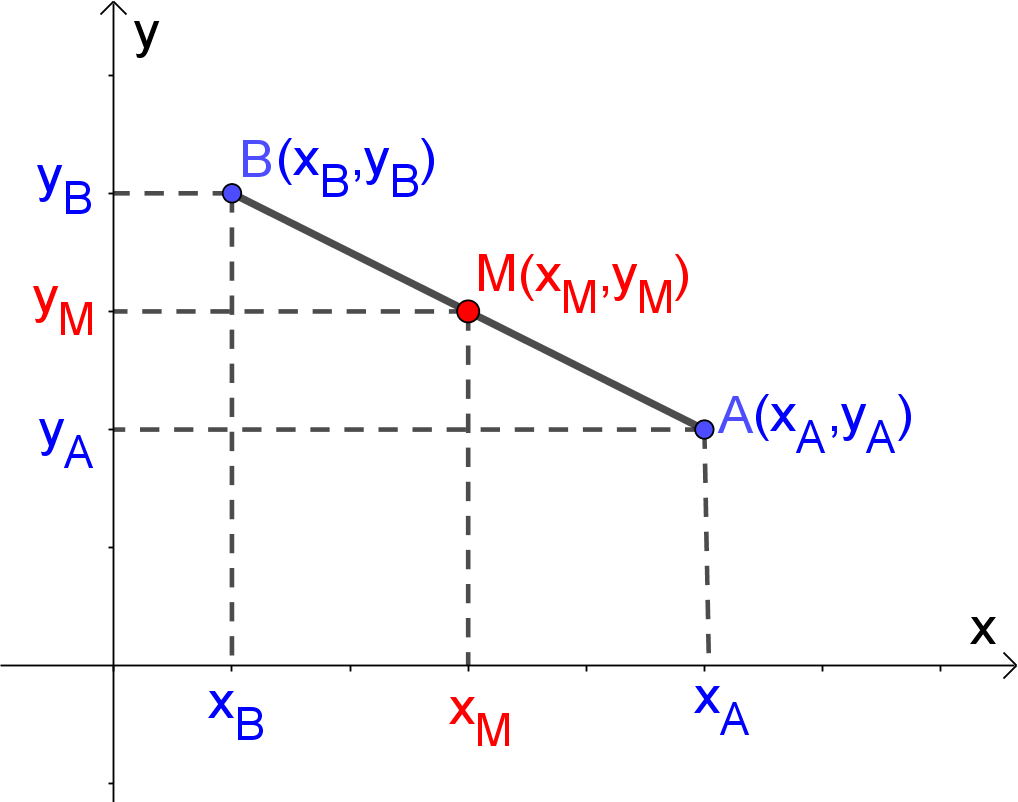Midpoint of Line Segment $M\Big(\frac{x_A+x_B}{2},\frac{y_A+y_B}{2}\Big)$
Input: Three non-collinear points $A(x_A,y_A), B(x_B,y_B)$ and $C(x_C, y_C)$	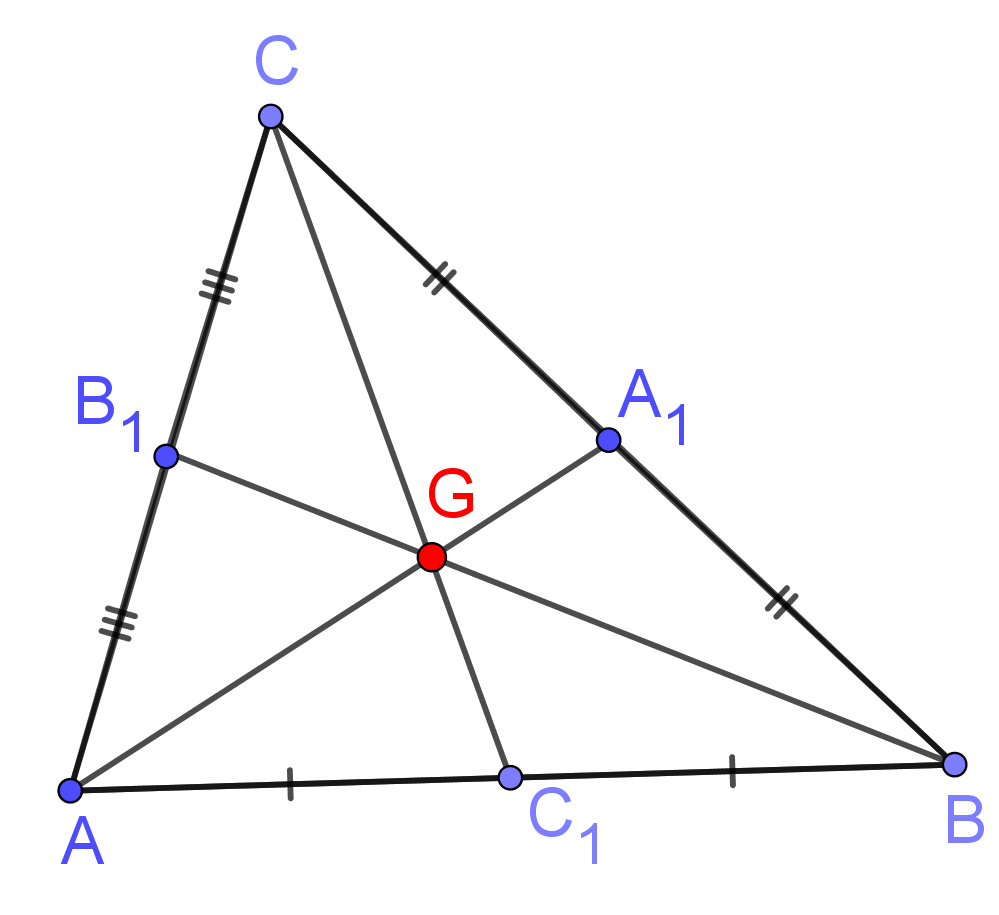Centroid Triangle $C\Big(\frac{x_A+x_B+x_C}{3},\frac{y_A+y_B+y_C}{3}\Big)$
Input: Point $A(x_A,y_A)$ and line $(p):Ax+By+C=0$	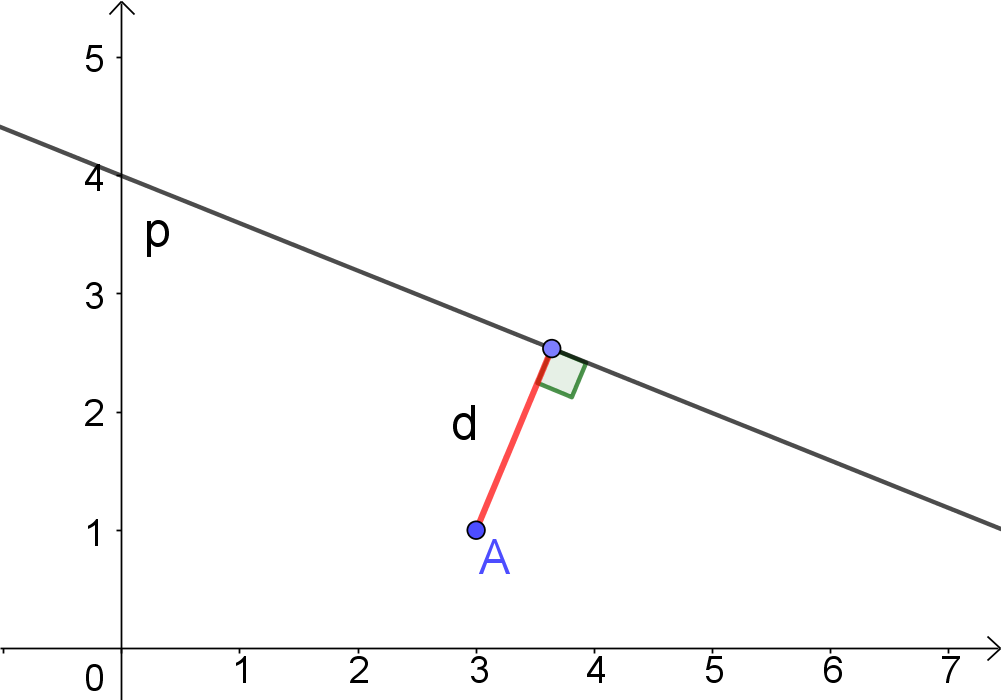Perpendicular Length $d(A,p)=\Big\|\frac{Ax_A+By_B+C}{\sqrt{A^2+B^2}}\Big\|$
Input: Point $A(x_A,y_A)$ and slope $m$	Point Slope Form $y-y_A=m(x-x_A)$
Input: Slope $m$ and intercept $b$	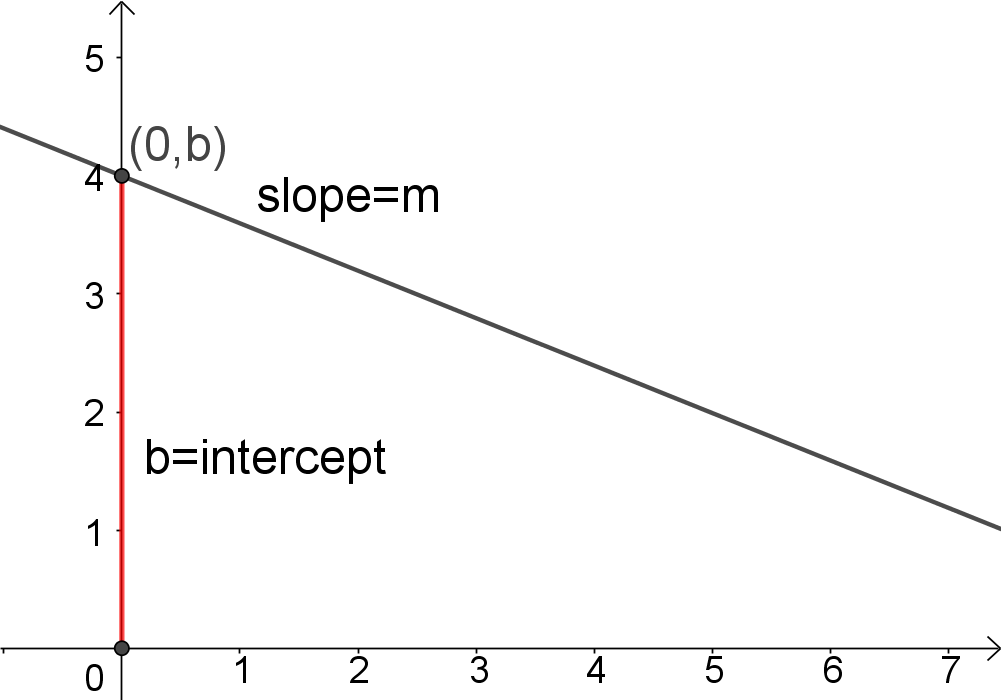Slope Intercept Form $y=mx+b$
Input: Two points $A(x_A,y_A)$ and $B(x_B,y_B)$	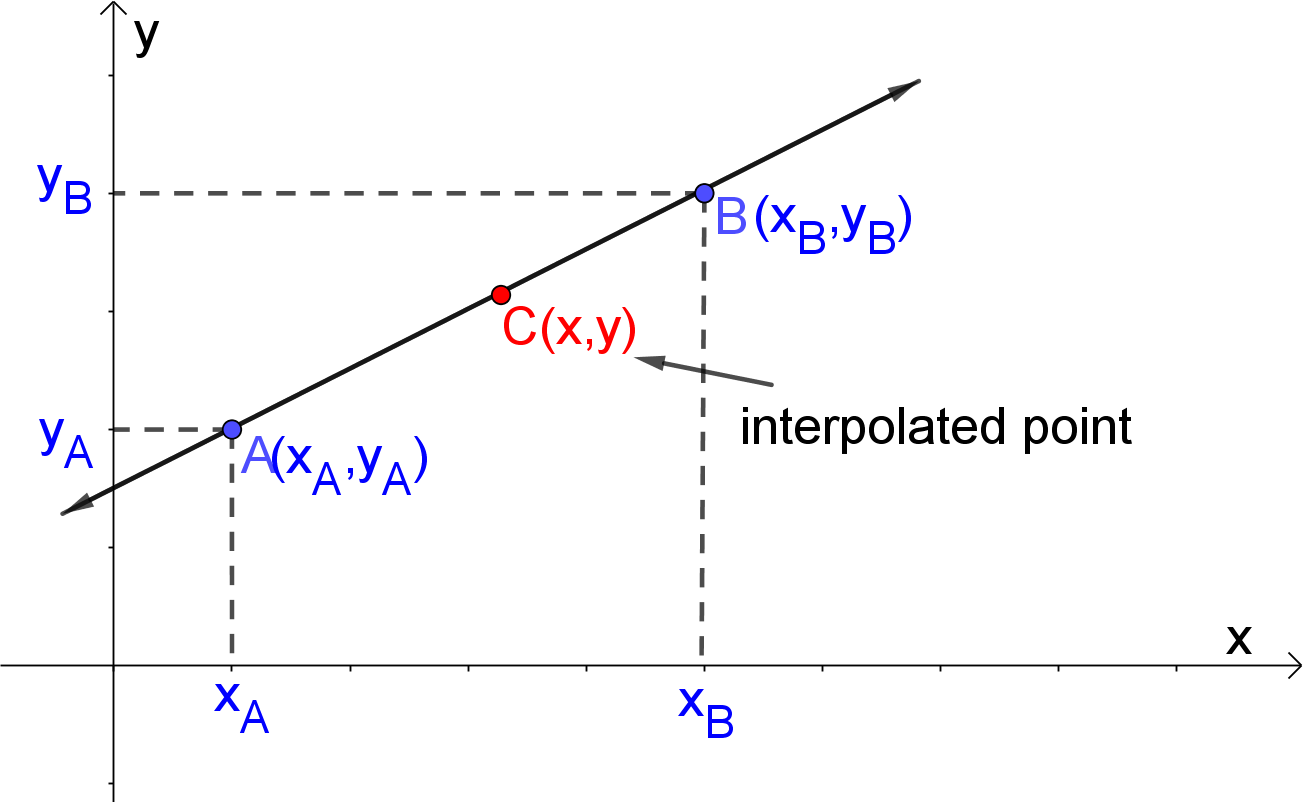Linear Interpolation $x_C=\frac{x_B(y_C-y_A)+x_A(y_B-y_C)}{y_B-y_A}$ $y_C=\frac{y_B(x_C-x_A)+y_A(x_B-x_C)}{x_B-x_A}$
Input: Three non-collinear points$A(x_A,y_A), B(x_B,y_B)$\ and $C(x_C, y_C)$	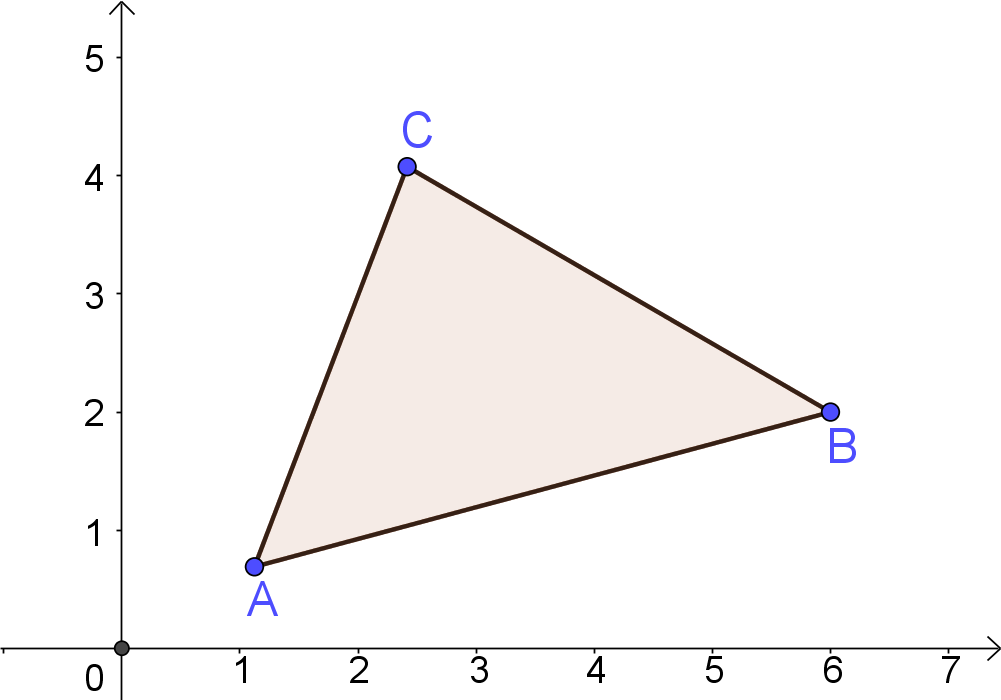Area of Triangle $A=\frac 12[x_A(y_B-y_C)+x_B(y_C-y_A)+x_C(y_A-y_B)]$
Input: Radius $r$ or Diameter $D$	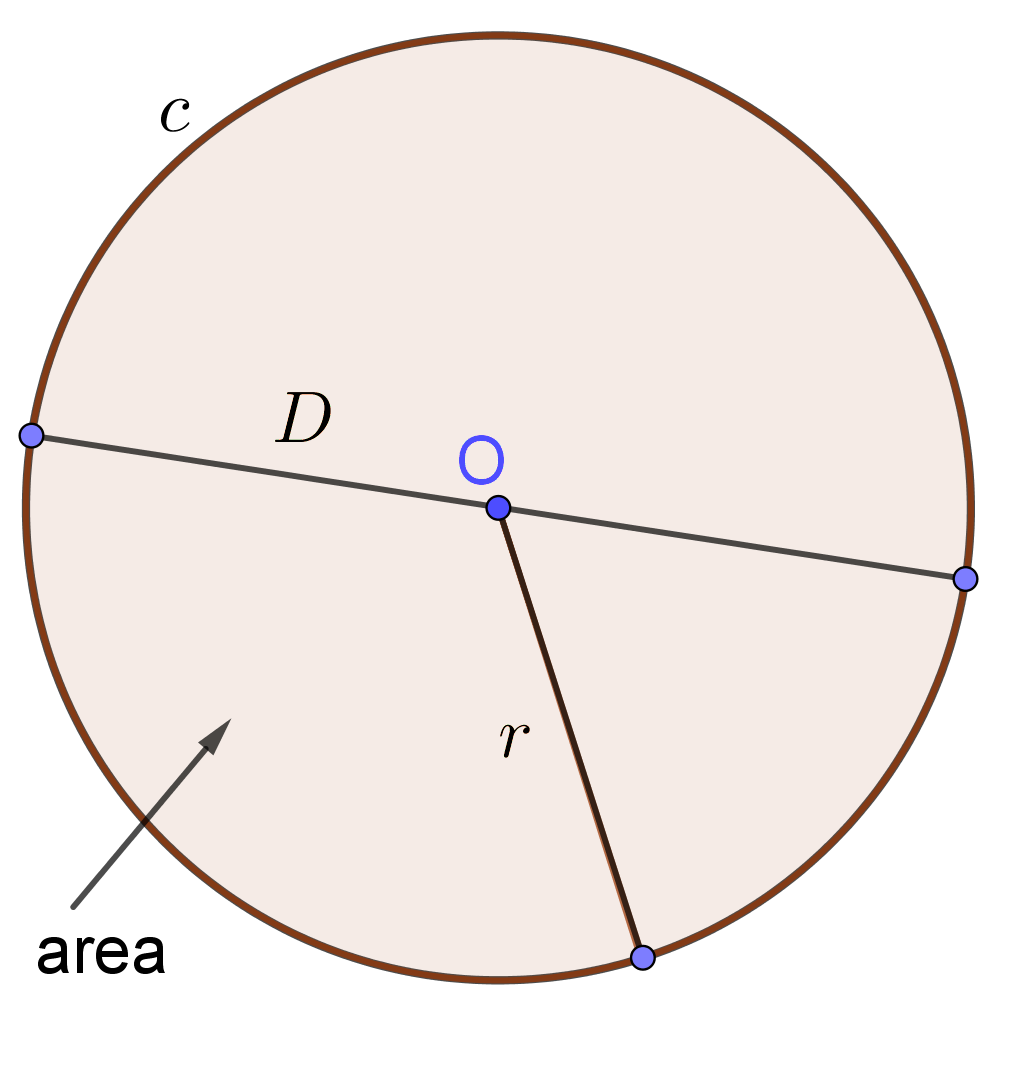Circle Formulas $\mbox{Area}=r^2\pi$ $\mbox{Diameter}\; D=2r$ $\mbox{Circumference}=2r\pi$
Input: Radius $r$ and central angle $\alpha$ in degrees of circular sector	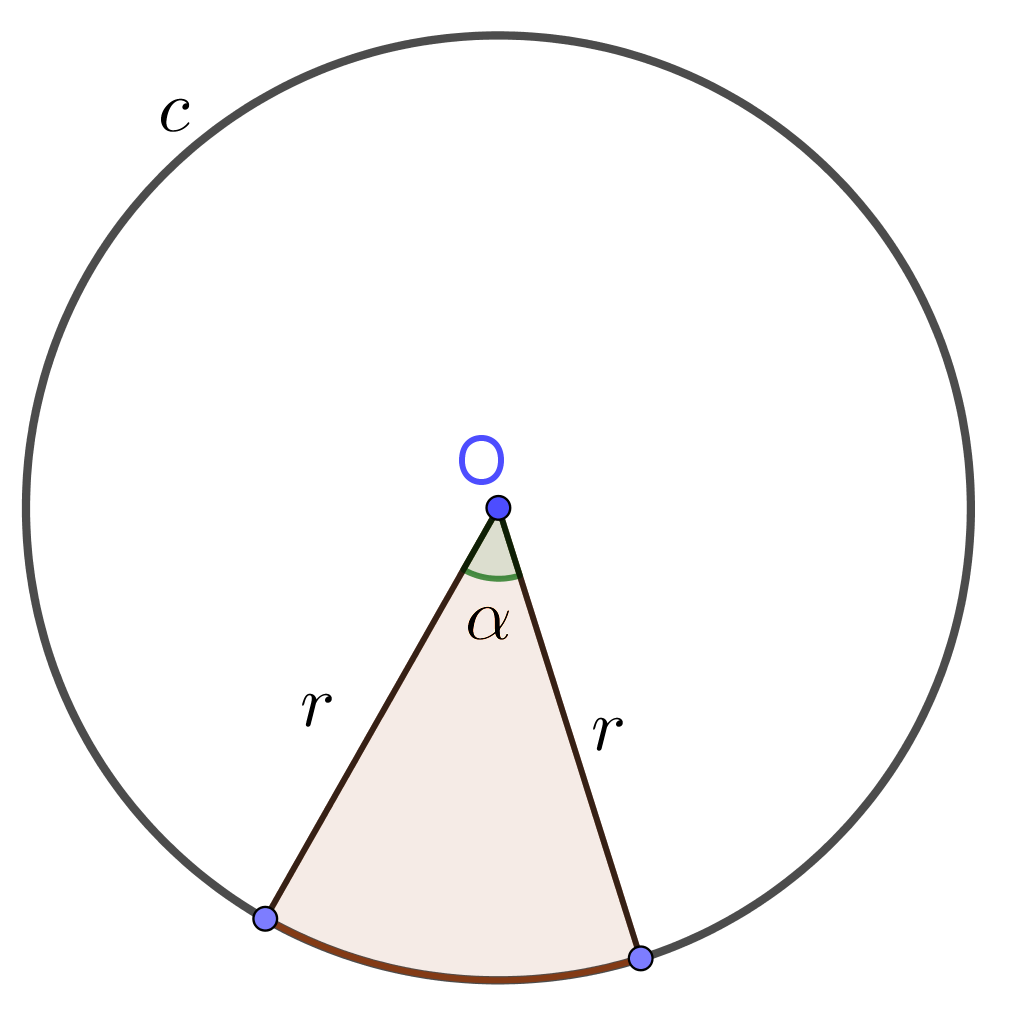Circular Sector Formula $\mbox{Area}=\frac{\pi r^2\alpha}{360^o}$
Input: Major radius $a$ and minor radius $ b $ of Ellipse	Ellipse Formulas $\mbox{Area}=\pi ab$ $\mbox{Perimeter}=2\pi\sqrt{\frac{a^2+b^2}{2}}$
Input: Side $a$ or diagonal $d$ of Square	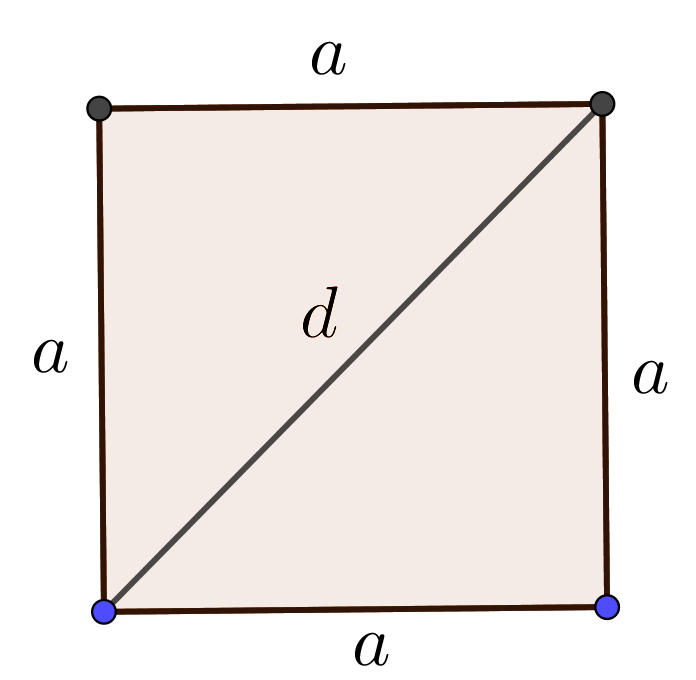Square Formulas $\mbox{Area}=a^2$ $\mbox{Perimeter}=4a$ $\mbox{Diagonal}\;d=\sqrt{2}a$
Input: Length $l$ and width $w$ of Rectangle	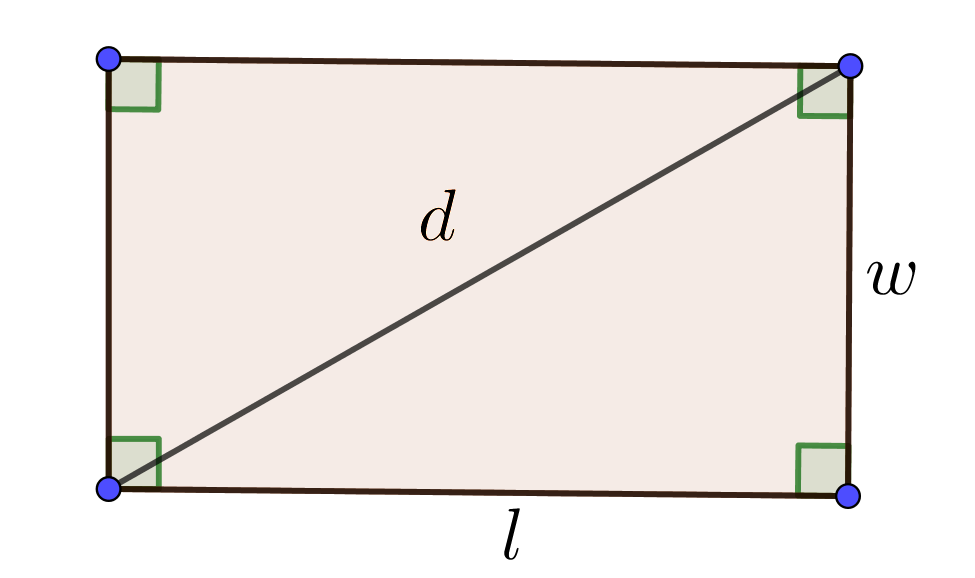Rectangle Formulas $\mbox{Area}=\mbox{length}\times\mbox{width}$=lw $\mbox{Perimeter}=2l+2w$ $\mbox{Diagonal}\;d=\sqrt{l^2+w^2}$
Input: Sides $a,b$ and $c$ of Triangle	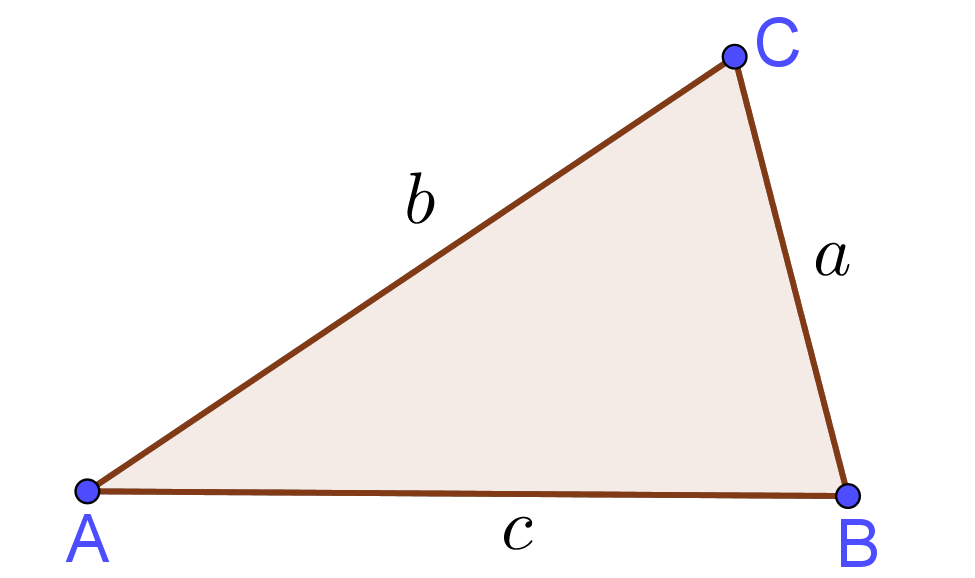Heron's Triangle Formula $\mbox{semiperimeter}\;s=\frac{a+b+c}{2}$ $\mbox{Area}=\sqrt{s(s-a)(s-b)(s-c)}$
Input: Base $c$ and its height $h$ of Triangle	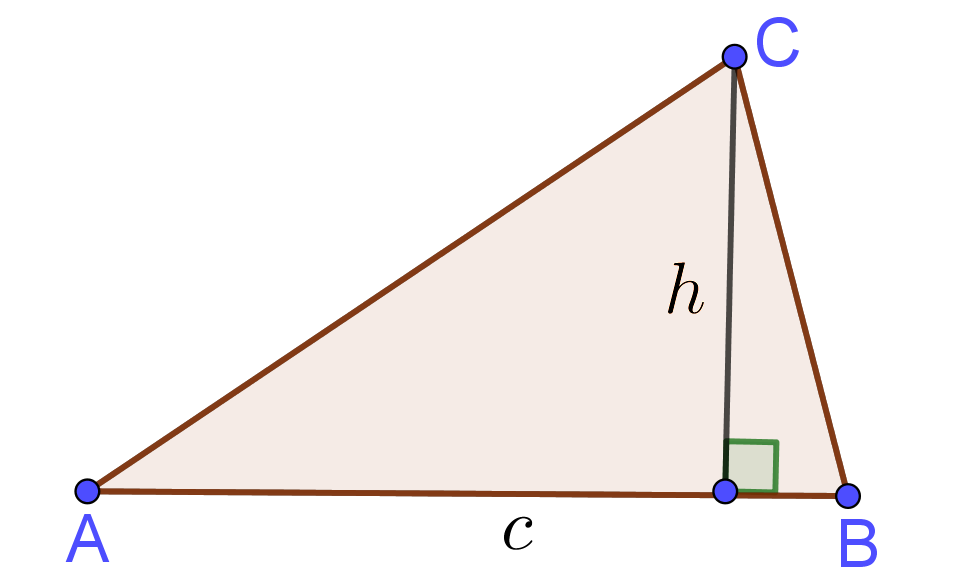Triangle Formula $\mbox{Area}=\frac{ch}{2}$
Input: Bases $a$ and $b$ and height $h$ of Trapezoid	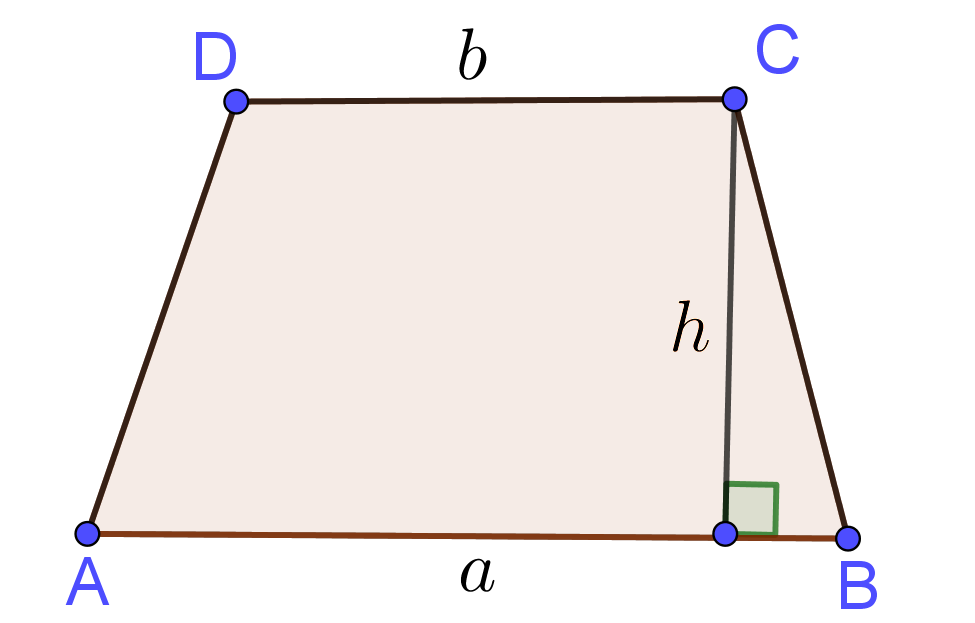Trapezoid Formula $\mbox{Area}=\frac{a+b}{2}h$
Input: Side $a$ and interior angle $\alpha$ or diagonals $d_1$ and $d_2$ of Rhombus	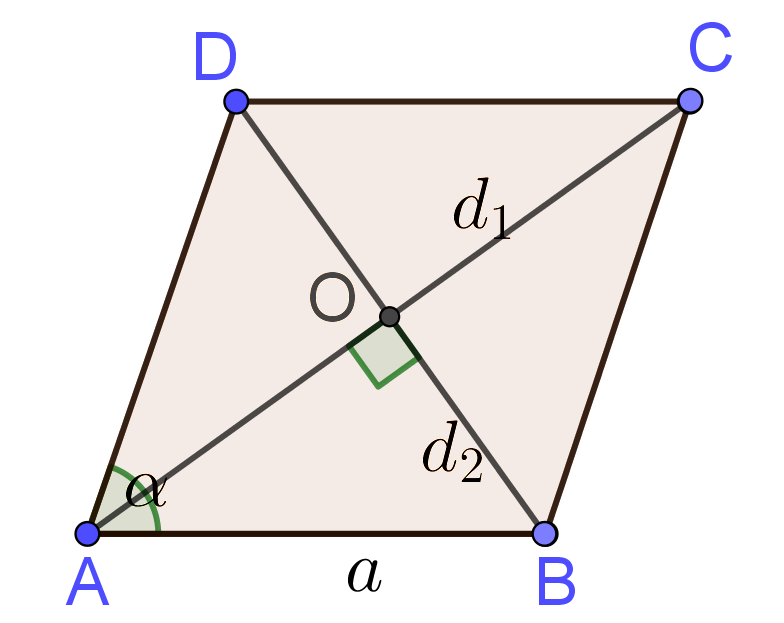Rhombus Formulas $\mbox{Area}=a^2\sin\alpha$ $\mbox{Area (diagonal method)}=\frac{d_1d_2}{2}$ $\mbox{Perimeter}=4a$
Input: Base $a$ and its height $h$ of Parallelogram	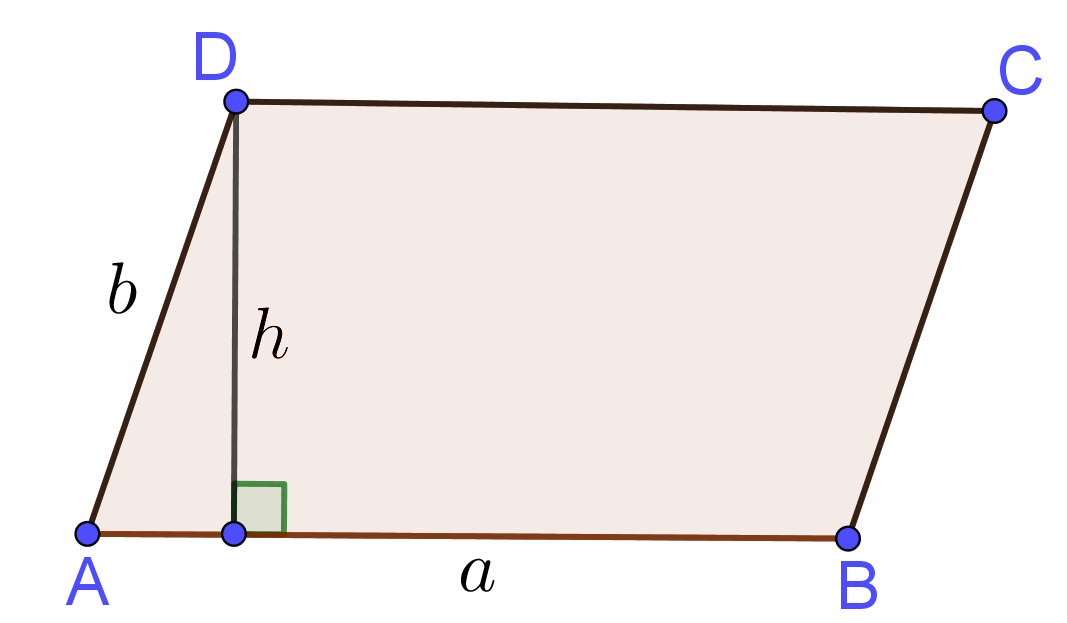Parallelogram Formulas $\mbox{Area}=\mbox{base}\times\mbox{height}={ah}$
Input: Radius $r$ or diameter $D$ of sphere	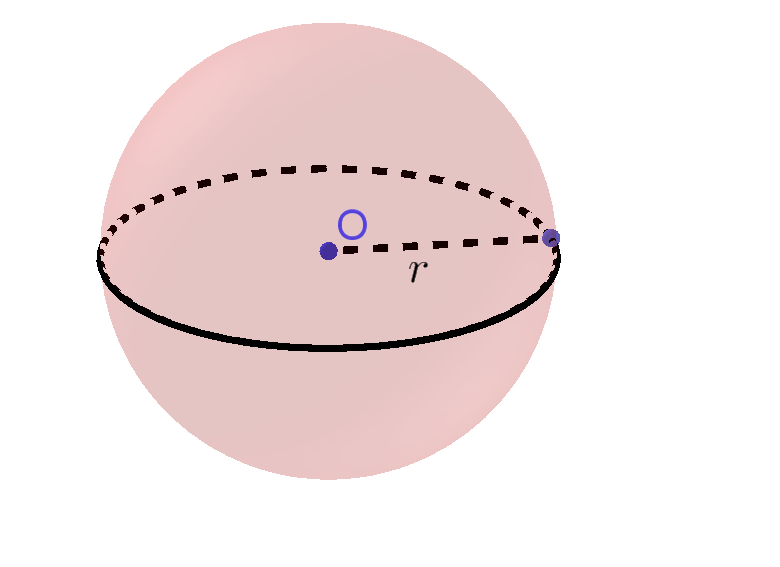Sphere Formulas $\mbox{Surface Area}=4\pi r^2=\pi D^2$ $\mbox{Volume}=\frac 43\pi r^3=\frac 16\pi D^3$
Input: Radius $r$ of Hemisphere	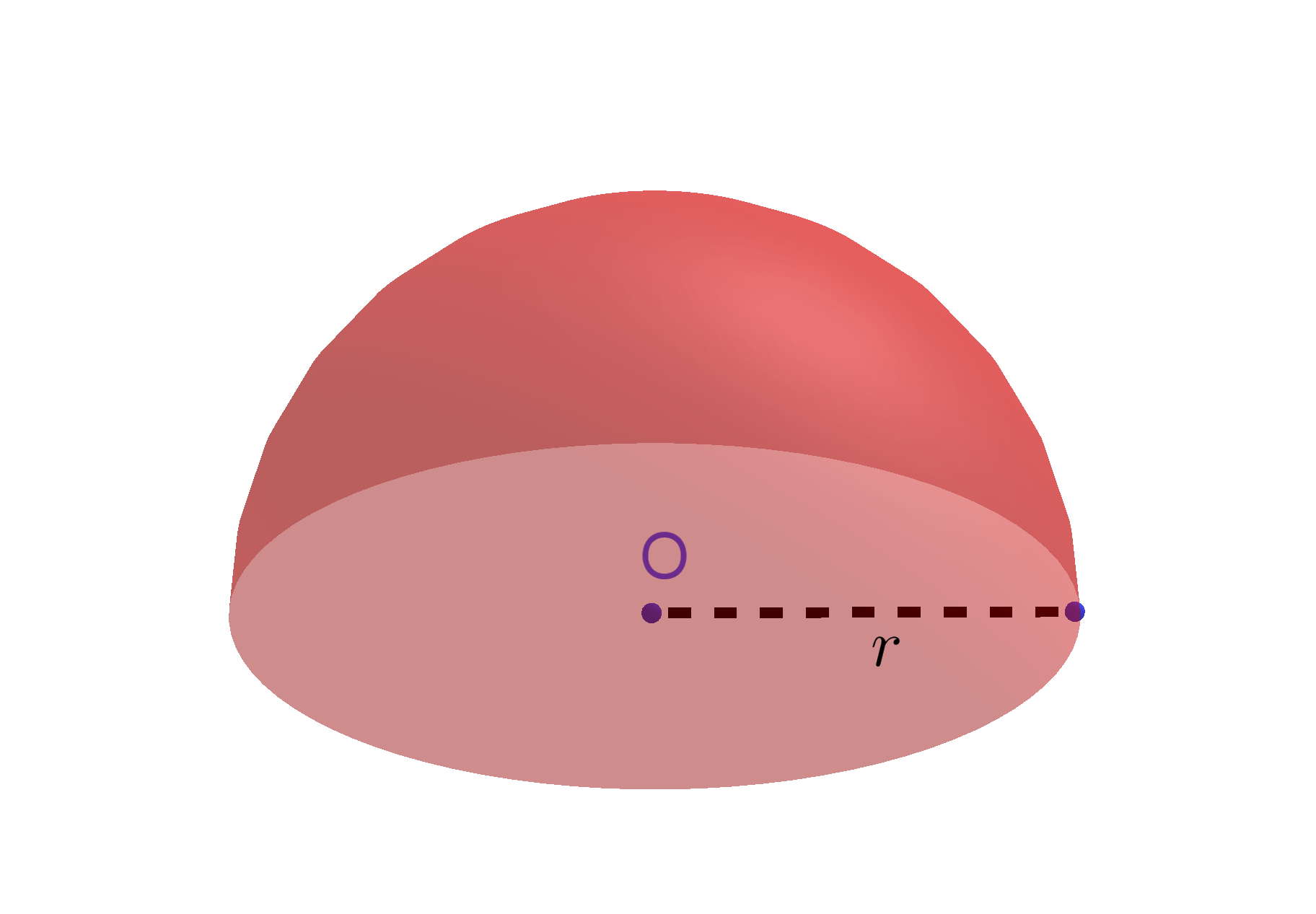Hemisphere Formulas $\mbox{Surface Area}=3\pi r^2$ $\mbox{Volume}=\frac 23\pi r^3$
Input: Base radius $r$ and height $h$ of Cone	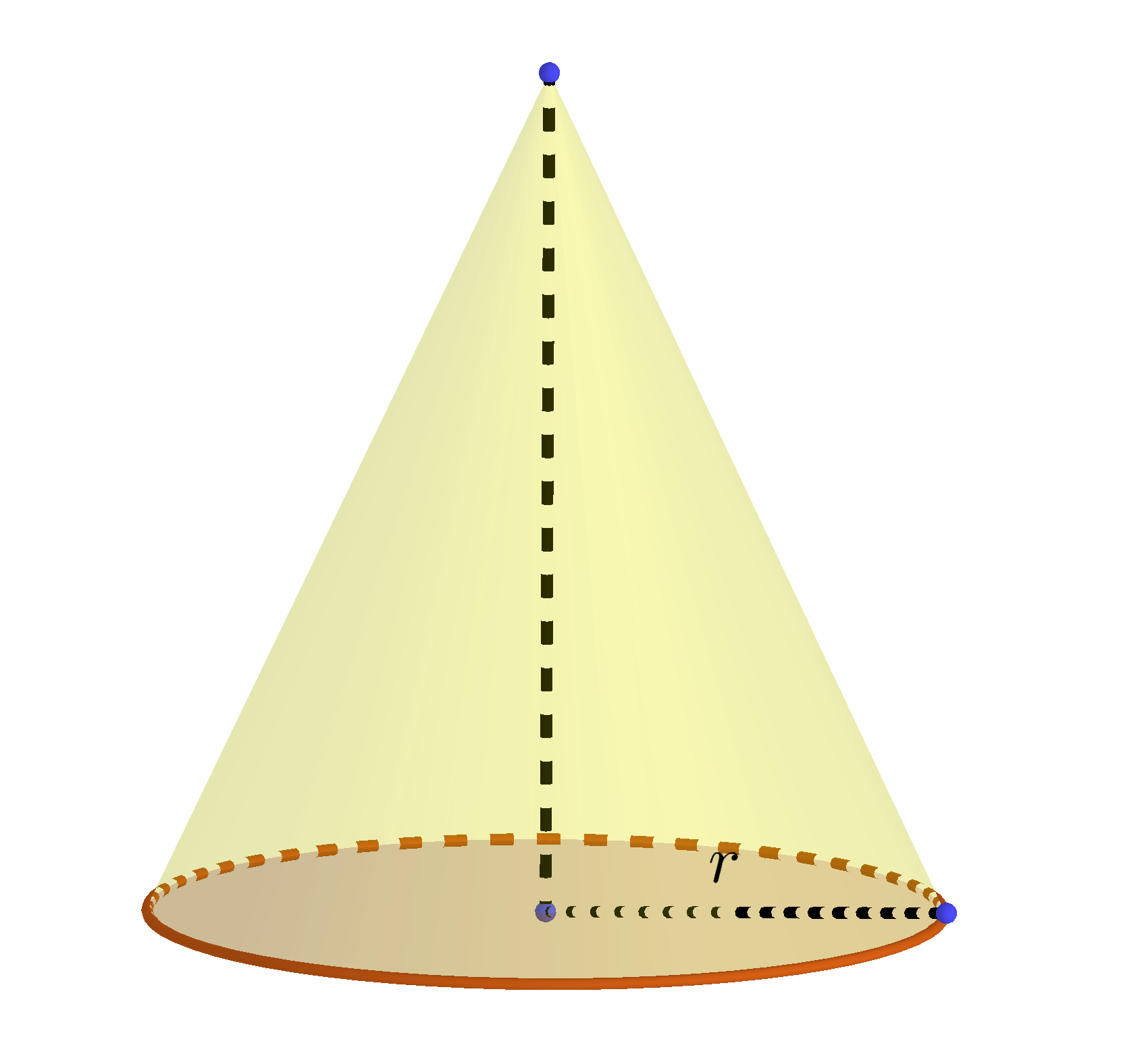Cone Formulas $\mbox{Surface Area}=\mbox{side area}+\mbox{base area}=\pi r(\sqrt{r^2+h^2}+r)$ $\mbox{Volume}=\frac 13\pi r^2h$ $\mbox{Slant Height}=\sqrt{r^2+h^2}$
Input: Base radius $r$ and height $h$ of Cylinder	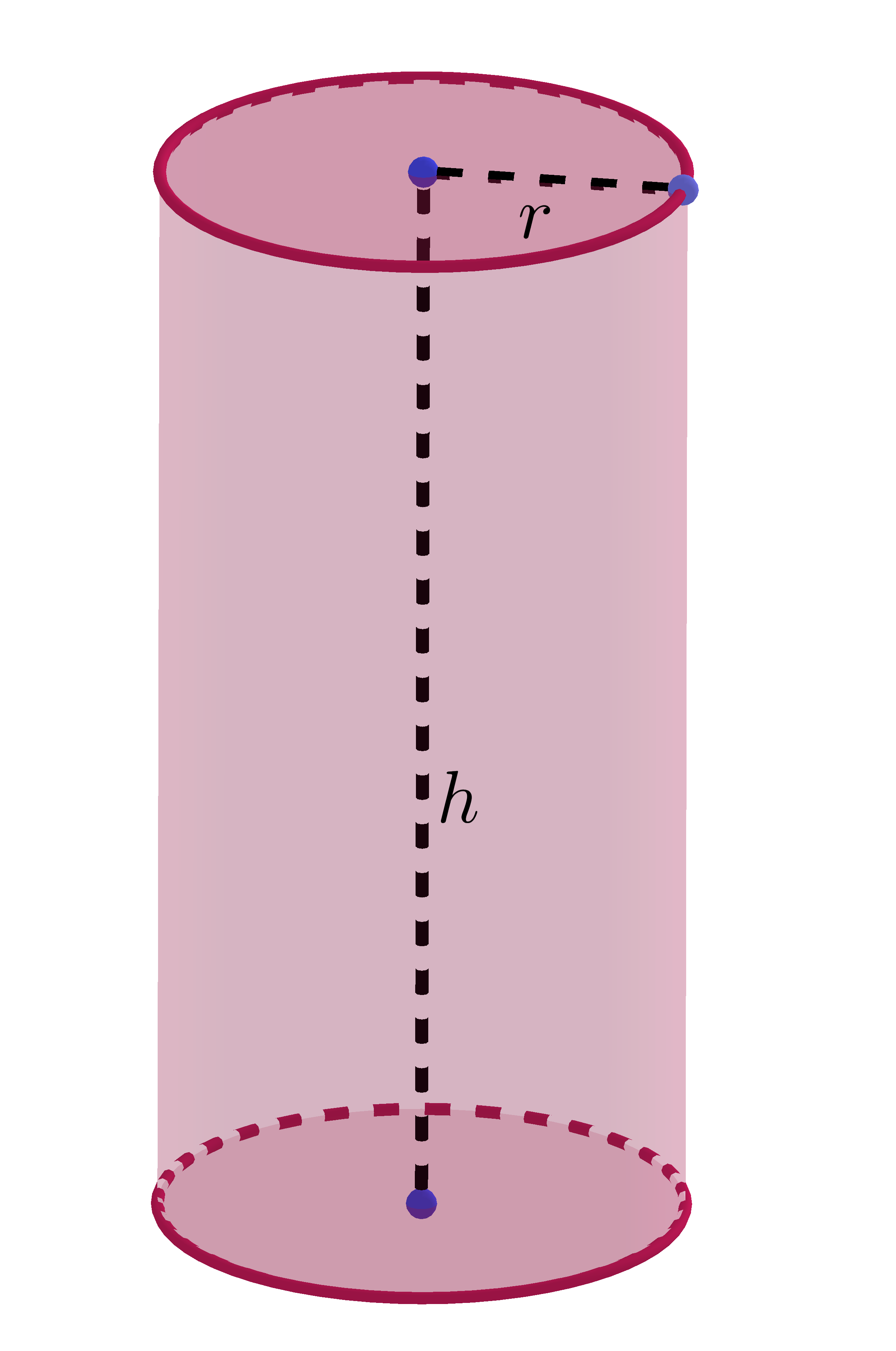Cylinder Formulas $\mbox{Surface Area}=2\pi r(r+h)$ $\mbox{Volume}=\pi r^2h$ $\mbox{Base surface area}=\pi r^2$ $\mbox{Lateral surface area}=2\pi rh$
Input: Side $a$ of Cube	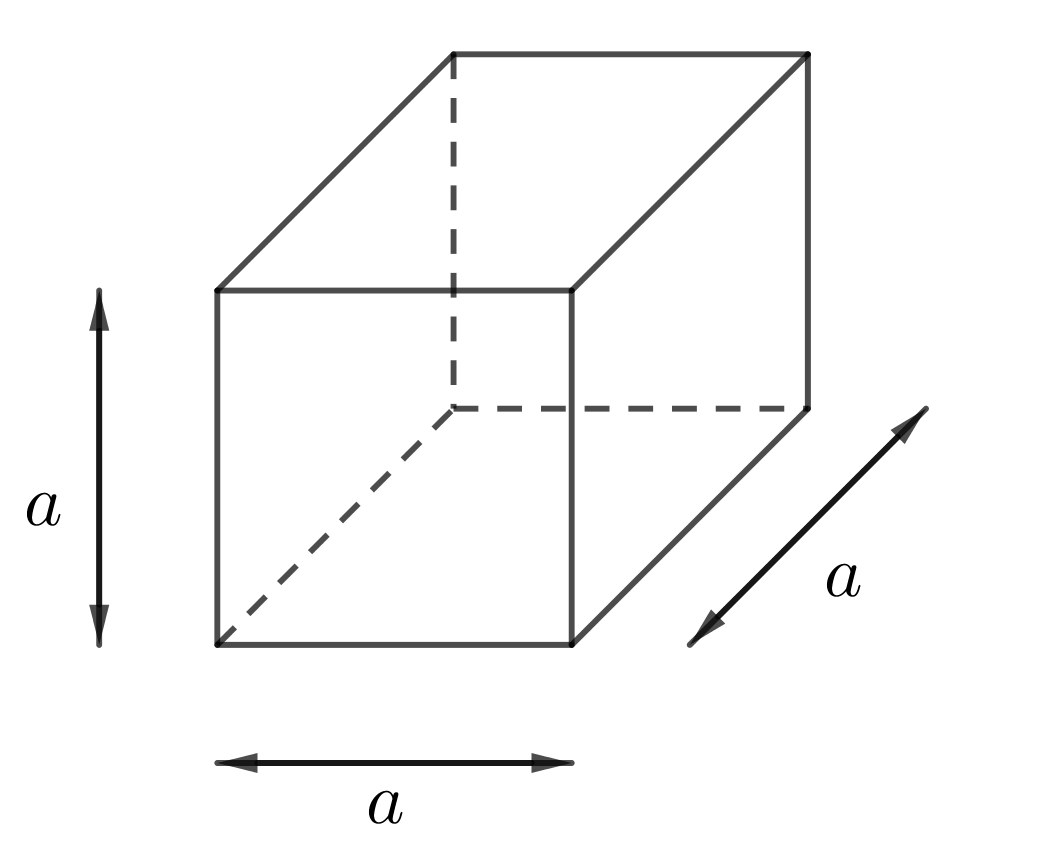Cube Formulas $\mbox{Area}=6a^2$ $\mbox{Volume}=a^3$
Input: Base side and height of Pyramid	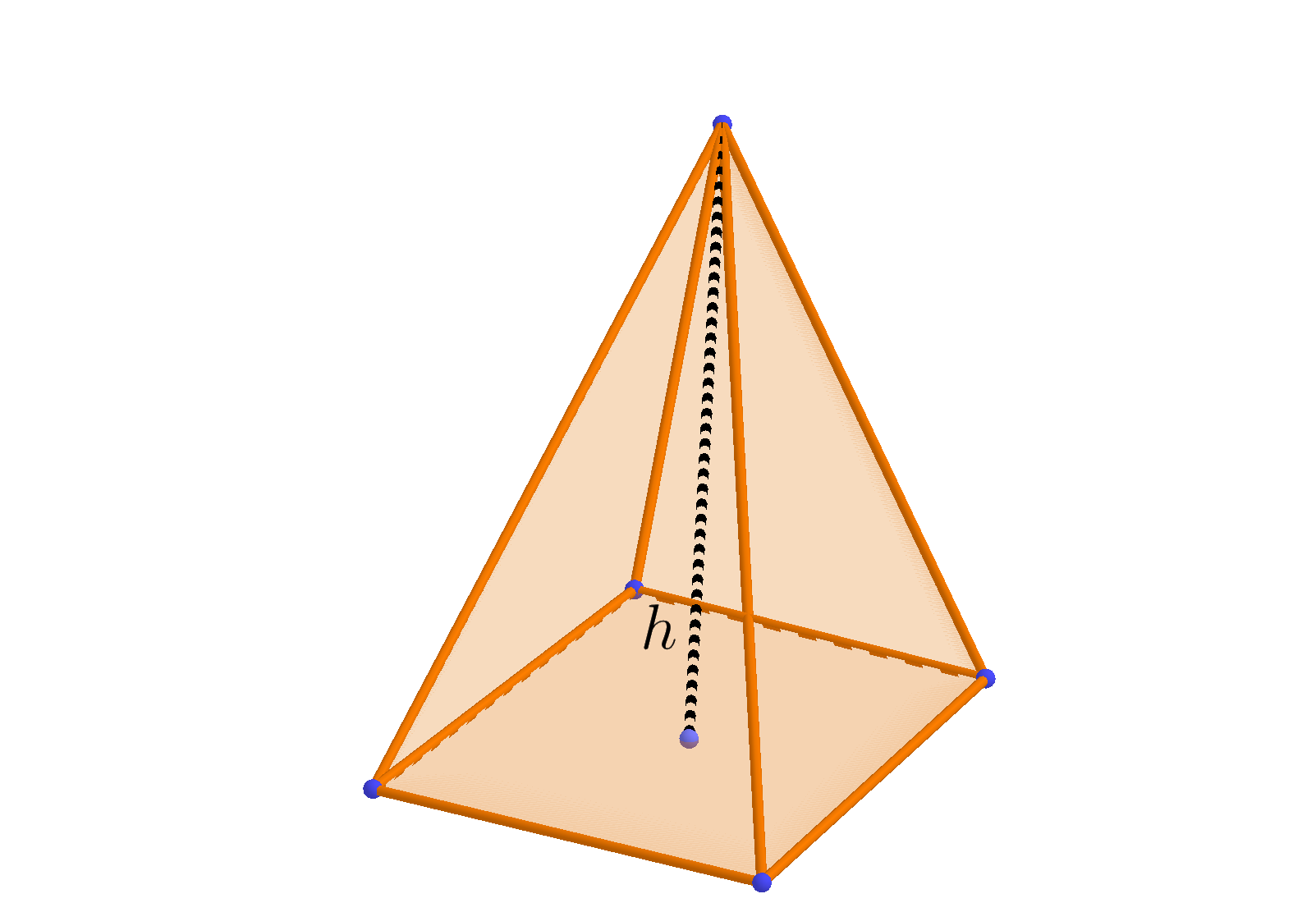Pyramid Formulas $\mbox{Surface Area}=\mbox{base area}+\frac 12\mbox{perimeter base}\times \mbox{slant height}$ $\mbox{Volume}=\frac 13\mbox{base area}\times\mbox{height}$
Input: Outer radius $R$, inner radius length $r$ and height $h$ of a Pipe	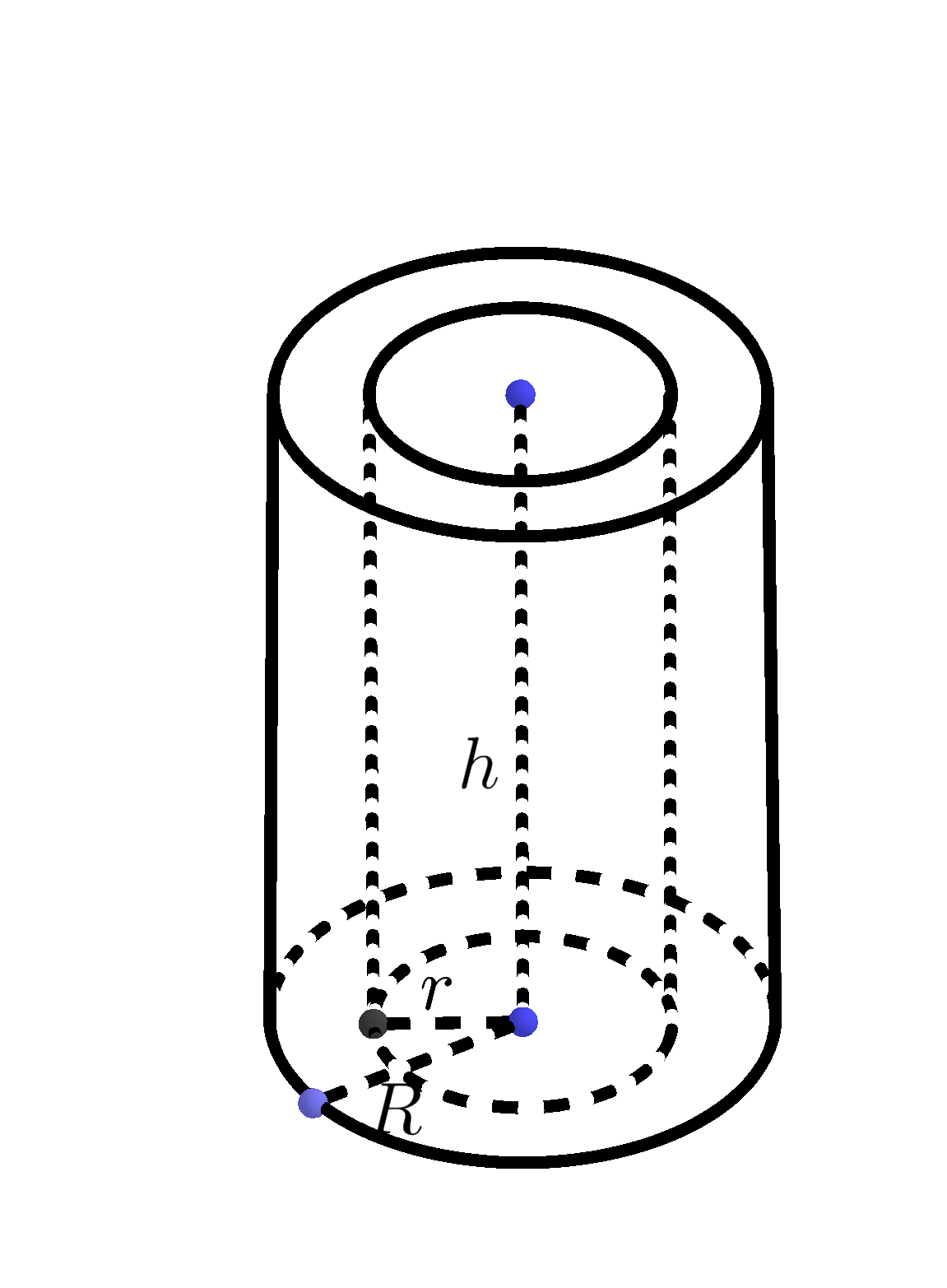Pipe Formulas $\mbox{Volume}=\pi(R^2-r^2) h$
Input: Base radius $r$ and height $h$ of Cylindrical Silo	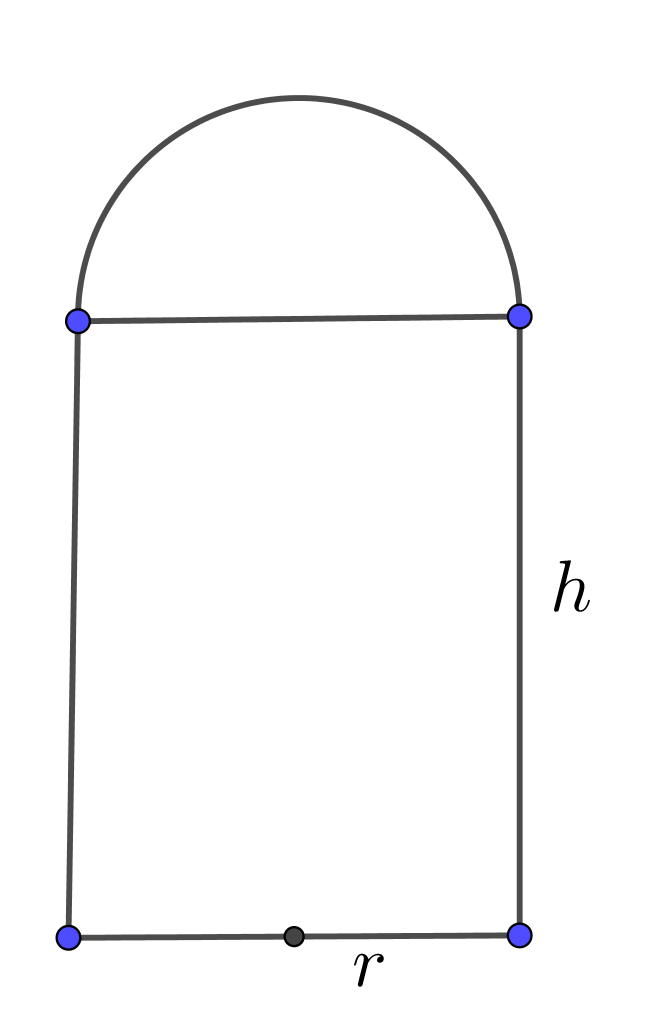Cylindrical Silo Formulas $\mbox{Volume}=\pi r^2h+\frac{2\pi r^3}3$
Input: Length $l$, width $w$ and height $h$ of Cuboid	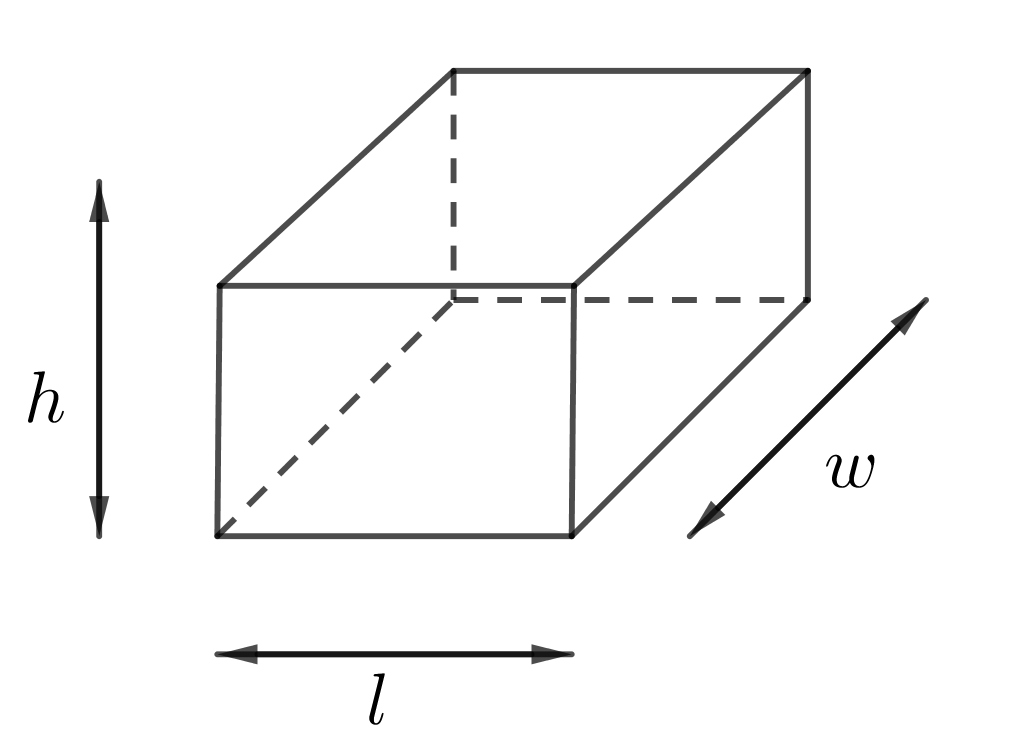Rectangular Cuboid Formulas $\mbox{Surface Area}=2(lw+hl+hw)$ $\mbox{Volume}=lwh$ $\mbox{Diagonal}=\sqrt{l^2+w^2+h^2}$ $\mbox{Length around edges}=4(l+w+h)$
Input: Middle radius $D$ top or bottom radius $d$ and height $h$ of Barrel	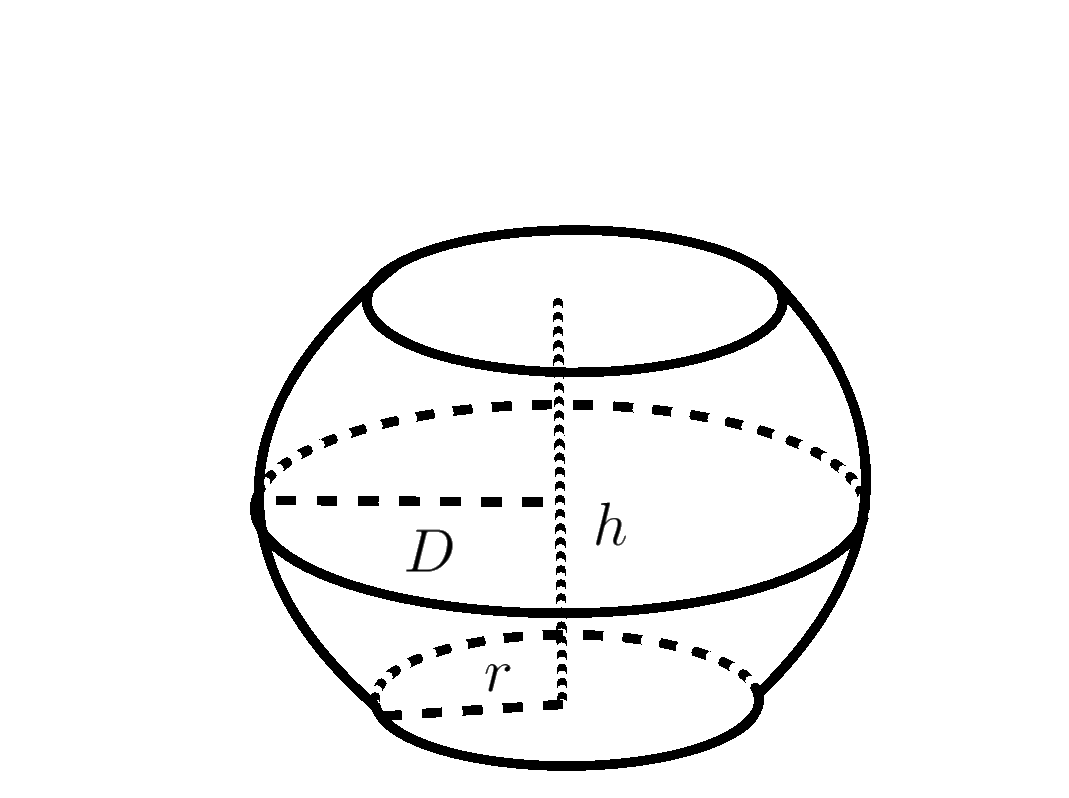Barrel Formulas $\mbox{Volume}=\frac{\pi h}{12} (2D^2+d^2)$

2D and 3D Geometry Formulas

Geometry Formulas Reference