nxn Inverse Matrix Calculator
nxn Inverse Matrix Calculator calculates a inverse of a square matrix $A$ with real elements. It is an online math tool specially programmed to calculate the inverse matrices of given 2x2, 3x3 and 4x4 matrices. Select the appropriate calculator from the list of three.
It is necessary to follow the next steps:
- Enter elements of matrix in the box. Elements of matrices must be real numbers.
- Press the "GENERATE WORK" button to make the computation;
- $n\times n$ inverse matrix calculator will give the matrix which represents the inverse matrix of the given matrix.
Output: A matrix with real elements.
Inverse Matrix Formula:
The inverse matrix of the matrix $A=\left( \begin{array}{cc} a & b \\ c &d \\ \end{array} \right)$ is determined by the following formula
The inverse matrix of the matrix $A=\left( \begin{array}{ccc} a & b & c \\ d& e & f \\ g & h & i \\ \end{array} \right)$ is determined by the following formula
The inverse matrix of the matrix $A=\left( \begin{array}{cccc} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \\ \end{array} \right)$ is determined by the following formula $$\begin{align} A^{-1}&=\frac{1}{det(A)}adj({A})\end{align}$$ where $adj({A})$ is the adjugate matrix of $A$. Adjugate matrix of $A$ is
What is Inverse Matrix?
A square matrix is a matrix with the same number of rows and columns. A square matrix with all elements as zeros except for the main diagonal, which has only ones, is called an identity matrix. The identity matrix for multiplication for any square matrix $A$ is the matrix $I$, such that $IA=A$ and $AI=A$. For instance, the following matrices
How to Find Inverse Matrix?
There are many different methods for finding the inverse of a given matrix. Some of them are: inverse of a matrix by Gauss-Jordan elimination and inverse of a matrix using minors, cofactors and adjugate. We will present the second one. The minor of an element of any $n\times n$ matrix is a $(n-1)\times (n-1)$ matrix determinant. If we delete the row and column containing the element, then we get appropriate minor. For example, the minor of the element $a$, element in the first row and first column, of the matrix
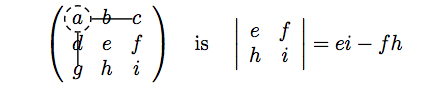
- If $det (A)\ne0$, the matrix $A$ is invertible;
- If $det (A)=0$, the matrix $A$ is not invertible or singular.
- Find the determinant of the matrix $A$, $det(A)$;
- Find the minors of the matrix $A$;
- Find the cofactor matrix,
- Find the adjugate;
- Inverse matrix of the matrix $A$ is the scalar multiplication of the adjugate by $\frac 1{det(A)}$.
Real World Problems Using Inverse Matrix
Using inverse of matrix, we can solve matrix equations of the types $$AX=B,\quad\mbox{and}\quad XA=B$$ for given matrices $A$ and $B$. If $A^{-1}$ exists, solutions of these equations are
Inverse Matrix Practice Problems
Practice Problem 1 :
Solve the matrix equation $\left(
\begin{array}{cc}
1 & 7 \\
-1 &3 \\
\end{array}
\right)X=\left(
\begin{array}{cc}
1& -1 \\
-2 &2\\
\end{array}
\right)$
Practice Problem 2:
Point $A'(3,5,1)$ is the image of the point $A$ after $90^o$ counterclockwise rotation about the origin $O$. Find the coordinate of the point $A$.
The nxn inverse matrix calculator, equations, example calculation, work with steps, real world problems and practice problems would be very useful for grade school students (K-12 education) to learn the concept of inverse matrix. This concept is conceived in almost all areas of science, so it will be helpful in solving more complex problems.
