Subtracting Fraction Calculator
Fraction Subtraction - work with steps
Input Data :
Fraction A = `8/7`
Fraction B = `3/4`
Objective :
Find what is fraction subtraction for given input data?
Solution :
A - B = `8/7 - 3/4`
denominator of the two fraction is different. Therefore, find lcm for two denominators (7, 4) = 28
Multiply lcm with both numerator & denominator
`8/7 - 3/4 = (8\times28)/(7\times28) - (3\times28)/(4\times28)`
= `(8\times4)/(28) - (3\times7)/(28)`
= `(32)/(28) - (21)/(28)`
Subtract two numerator of the fraction
`(32)/(28) - (21)/(28) = (32 - 21)/28 = 11/28`
`8/7-3/4 = 11/28`
Fractions subtraction calculator uses two proper or improper fractions, $\frac{a}{b}$ and $\frac{c}{d}$ for $b,d\ne0$, and calculates their difference.
It is an online tool for finding the difference in the simplest form of two proper or improper fractions.
It is necessary to follow the next steps:
- Enter two fractions $\frac{a}{b}$ and $\frac{c}{d}$ in the box. The numbers $a,b,c$ and $d$ must be integers such that $b$ and $d$ must be nonzero.
- Press the "GENERATE WORK" button to make the computation;
- Fraction subtraction calculator will give the difference between the first fraction and the second fraction.
Output: A fraction in the simplest form.
Fractions Subtraction Rule:
- If denominators are equal, $b=d$:
$$\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b},\quad \mbox{for}\;b\ne0$$
- If denominators are different, $b\ne d$:
$$\frac{a}{b}-\frac{c}{d}=\frac{a\times d-c\times b}{b\times d},\quad \mbox{for}\;b,d\ne0$$or equivalently,$$\frac{a}{b}-\frac{c}{d}=\frac{a\times \frac{LCM(b,d)}{b}-c\times \frac{LCM(b,d)}{d}}{LCM(b,d)},\quad \mbox{for}\;b,d\ne0$$where $LCM(b,d)$ is the least common multiple of $b$ and $d$.
How to Subtract Fractions?
The result in the subtraction of numbers is \underline{a difference}. A difference of two numbers depends on their order, i.e.
the subtraction is non-commutative operation. For example, $\frac 53-\frac 13\ne \frac 13-\frac 53$.
Like the commutative property, the associative property is not satisfied for the subtraction of numbers.
When we deal with fractions, there are two types of subtraction:
- When denominators are equal
- When denominators are different
- Find the LCM of denominators;
- Rewrite the fractions over the LCM;
- Subtract new numerators;
- The result is the difference of numerators over the LCM;
- Simplify the result if needed.
The fraction subtraction work with steps shows the complete step-by-step calculation for finding the difference of two fractions $\frac{7}{6}$ and $\frac{3}{4}$ using the fractions subtraction rule. For any other fractions, just supply two proper or improper fractions and click on the GENERATE WORK button. The grade school students may use this subtracting like or unlike fraction calculator to generate the work, verify the results of subtracting two or more numbers derived by hand or do their homework problems efficiently.
Real World Problems Using Fractions Subtraction
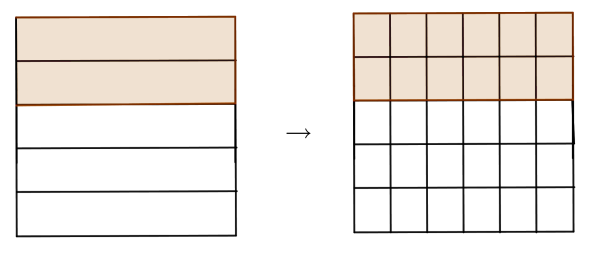
Because many real-life situations deal with fractions, subtracting of fractions is very useful. The subtraction of fractions can be represented by area model.For example, let us find the difference $\frac 2 5-\frac 16$.
If we divide a square into five congruent rectangles, $\frac 25$ means $2$ rectangles of the square.
Further, by dividing the same square into $30$ rectangles $12$ shared rectangles have equal area as $2$ previously shared rectangles. So, $\frac 2 5$ is equal to $\frac {12} {30}$.
In the same manner, we can rewrite the fraction $\frac 16$ as $\frac 5{30}$.

Since both fractions have the same common denominator, we can find the difference between the first fraction $\frac{12}{30}$ and the second fraction $\frac {5}{30}$. If we subtract rectangles on the first picture with the rectangle on the second picture, we get $7$ shared rectangles. So, the difference is $\frac {7}{30}.$
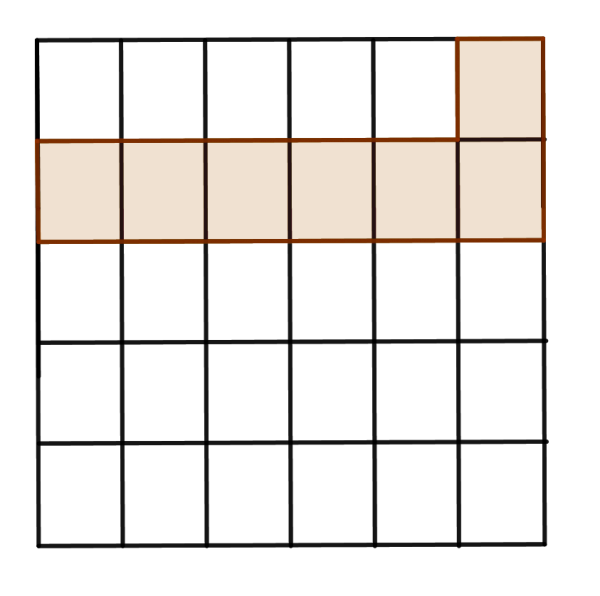
Fraction Subtraction Practice Problems
Practice Problem 1:
John walked $\frac {6}{15}$ of a path and then run $\frac 13$ of a path. How much farther did he walk than run?
Practice Problem 2:
We had $\frac {185}3$ grams of sugar. Then we used $\frac{123}{5}$ grams to make a cake. How much sugar we have left?
The fraction subtraction calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the subtraction of two numbers represented as fractions. Using this concept they can be able to solve complex algebraic problems and equations as well as real life problems.
| Like & Unlike Fractions Subtraction | |
|---|---|
| Fractions | Difference |
| 9/4 - 9/8 | 9/8 |
| 5/6 - 5/9 | 5/18 |
| 7/9 - 7/2 | -49/18 |
| 3/5 - 1/7 | 16/35 |
| 2/3 - 6/7 | -4/21 |
| 2/9 - 1/4 | -1/36 |
| 7/9 - 3/7 | 22/63 |
| 4/9 - 4/3 | -8/9 |
| 8/5 - 9/5 | -1/5 |
| 5/7 - 2/5 | 11/35 |
| 4/5 - 7/8 | -3/40 |
| 9/4 - 1/5 | 41/20 |
| 7/9 - 1/2 | 5/18 |
| 5/9 - 4/3 | -7/9 |
| 3/5 - 1/6 | 13/30 |
| 5/6 - 5/3 | -5/6 |
| 7/6 - 7/3 | -7/6 |
| 4/7 - 7/8 | -17/56 |
| 8/5 - 7/4 | -3/20 |
| 7/4 - 8/5 | 3/20 |
| 7/2 - 1/2 | 3/1 |
| 1/6 - 3/4 | -7/12 |
| 1/7 - 7/2 | -47/14 |
| 3/4 - 5/7 | 1/28 |
| 9/8 - 9/4 | -9/8 |
| 9/8 - 3/2 | -3/8 |
| 1/8 - 1/4 | -1/8 |
| 7/2 - 8/3 | 5/6 |
| 2/7 - 2/5 | -4/35 |
| 4/7 - 3/8 | 11/56 |
| 7/5 - 5/4 | 3/20 |
| 1/9 - 8/9 | -7/9 |
| 8/9 - 7/8 | 1/72 |
| 1/3 - 7/5 | -16/15 |
| 8/7 - 7/4 | -17/28 |
| 8/7 - 7/9 | 23/63 |
| 5/8 - 5/3 | -25/24 |
| 4/5 - 3/7 | 13/35 |
| 4/5 - 3/5 | 1/5 |
| 3/4 - 4/3 | -7/12 |
| 1/3 - 7/4 | -17/12 |
| 6/5 - 6/7 | 12/35 |
| 3/7 - 1/9 | 20/63 |
| 4/7 - 2/9 | 22/63 |
| 7/4 - 1/8 | 13/8 |
| 7/5 - 5/9 | 38/45 |
| 2/3 - 8/5 | -14/15 |
| 7/6 - 6/5 | -1/30 |
| 8/3 - 4/7 | 44/21 |
| 9/7 - 1/9 | 74/63 |
| 1/5 - 2/7 | -3/35 |
| 7/8 - 5/9 | 23/72 |
| 8/5 - 5/7 | 31/35 |
| 2/5 - 7/8 | -19/40 |
| 5/6 - 5/2 | -5/3 |
| 7/5 - 7/9 | 28/45 |
| 3/2 - 6/5 | 3/10 |
| 6/5 - 1/7 | 37/35 |
| 2/9 - 4/5 | -26/45 |
| 4/7 - 9/8 | -31/56 |
| 3/8 - 1/6 | 5/24 |
| 2/5 - 4/3 | -14/15 |
| 9/7 - 4/5 | 17/35 |
| 2/9 - 1/3 | -1/9 |
| 3/4 - 1/3 | 5/12 |
| 8/9 - 6/7 | 2/63 |
| 7/3 - 6/5 | 17/15 |
| 2/3 - 1/2 | 1/6 |
| 7/8 - 4/3 | -11/24 |
| 4/9 - 7/6 | -13/18 |
| 5/2 - 3/5 | 19/10 |
| 2/9 - 5/2 | -41/18 |
| 2/3 - 2/7 | 8/21 |
| 7/6 - 5/8 | 13/24 |
| 1/5 - 3/4 | -11/20 |
| 1/8 - 5/8 | -1/2 |
| 7/2 - 2/9 | 59/18 |
| 6/5 - 1/9 | 49/45 |
| 2/7 - 1/4 | 1/28 |
| 2/7 - 8/9 | -38/63 |
| 6/5 - 5/8 | 23/40 |
| 9/8 - 3/8 | 3/4 |
| 9/4 - 1/6 | 25/12 |
| 4/5 - 3/8 | 17/40 |
| 8/9 - 1/3 | 5/9 |
| 7/3 - 6/7 | 31/21 |
| 1/7 - 5/6 | -29/42 |
| 5/9 - 9/4 | -61/36 |
| 8/3 - 1/7 | 53/21 |
| 2/5 - 7/9 | -17/45 |
| 5/3 - 3/8 | 31/24 |
| 9/4 - 8/3 | -5/12 |
| 1/8 - 2/3 | -13/24 |
| 1/9 - 7/4 | -59/36 |
| 2/5 - 1/9 | 13/45 |
| 1/7 - 5/3 | -32/21 |
| 9/4 - 3/4 | 3/2 |
| 3/8 - 1/3 | 1/24 |
| 5/3 - 1/7 | 32/21 |
| 4/9 - 1/9 | 1/3 |
