Heron's Triangle Area Calculator
Heron's triangle area calculator - step by step calculation, formula & solved example problem to find the area for the given values of a, b & c of triangle in different measurement units between inches (in), feet (ft), meters (m), centimeters (cm) & millimeters (mm). The formulas, solved example & step by step calculations may useful for users to understand how the input values are being used in heron's triangle area calculations. Also this featured calculator uses the various conversion functions to find the triangle area & semi-perimeter in SI or metric or US customary units.
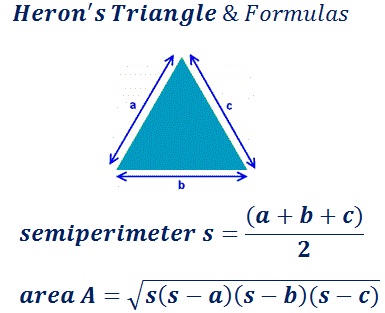
Heron's Triangle & its Formulas
The following mathematical formula is used in this calculator to find the area & semi-perimeter of a triangle for the given input value of side lengths a, b & c.
Solved Example
The below solved example problem may be useful to understand how the values are being used in the mathematical formulas to find the heron's triangle area.
Example Problem :
Find the area of a triangle having the side lengths a = 18 cm, b = 12 cm & c = 10 cm?
Solution :
The given values
length a = 18 cm
length b = 12 cm
length c = 10 cm
Step by step calculation
formula to find semi-perimeter s = (a + b +c)/2
substitute the values
= (18 + 12 + 10)/2
= 20 cm
heron's formula to find area = √s(s - a)(s - b)(s - c)
substitute the values
= √20 x (20-18) x (20-12) x (20-10)
= √20 x 2 x 8 x 10
= 56.56 cm
The area of a triangle may required to be calculated in SI or metric or US customary unit systems, therefore this heron's triangle area calculator is featured with major measurement units conversion function to find the output values in different customary units such as inches (in), feet (ft), meters (m), centimeters (cm) & millimeters (mm) by using this below conversion table.
| 10 mm = 1 cm 100 mm = 3.93 in 1000 mm = 3.28 ft 1000 mm = 1 m |
1 cm = 10 mm 10 cm = 3.93 in 100 cm = 3.28 ft 100 cm = 1 m |
1 ft = 3048 mm 1 ft = 304.8 cm 1 ft = 12 in 10 ft = 3.048 m |
1 in = 25.4 mm 1 in = 2.54 cm 100 in = 8.33 ft 100 in = 2.54 m |
In the field of area & volume calculations, finding the area of triangle is very important to understand the element of basic mathematics. The above formulas, step by step calculation & solved example may helpful for users to understand the how to calculate the area of triangle manually, however, when it comes to online to perform quick calculations, this Heron's triangle calculator may be useful to find the results.
