Area and Perimeter of Polygon Calculator

Number of sides

Side length

Polygon name = Pentagon

Sum of interior angle = 540

Interior angle = 108

Exterior angle = 72

Perimeter = 50

Area = 172.0477

GENERATE WORK

CALCULATE

Polygon Name, Edges, Angle, Area & Perimeter - work with steps

Input Data :
Number of sides n = 5
Side length l = 10

Objective :
Find what is the interior angle, exterior angle, area & perimeter of the polygon?

Solution :
Interior Angle = (n - 2) x 180n
= (5 - 2) x 1805
= 3 x 1805
= 5405
Interior Angle = 108

Sum of Interior Angle = (n - 2) x 180
= (5 - 2) x 180
= (3) x 180
Sum of Interior Angle = 540

Exterior Angle = 360n
= 3605
Exterior Angle = 72

Perimeter = Side x Side Length
= 5 x 10
Perimeter = 50

Area = Side Length x (Perimeter/2)2 tan(180/n)
= 10 x (50/2)2 tan (180/5)
= 10 x 252 tan (36)
= 2502 x 0.7265
= 2501.4531
Area = 172.0477

Area and perimeter of polygon calculator uses two parameters, number of sides and side length of a regular polygon, and calculates the sum of interior angles, measures of interior and exterior angles, perimeter and area of the polygon. It is an online Geometry tool requires number of sides and side length of a regular polygon. Using this polygon calculator, we will understand methods of how to find the sum of interior angles, measures of interior and exterior angles, perimeter and area of any regular polygon.
It is necessary to follow the next steps:

Enter the number of sides and the side length of a regular polygon in the box. The number of sides must be an integer, while the value of side length of a regular polygon must be positive real number or parameter. Note that the length of a segment is always positive;
Press the "GENERATE WORK" button to make the computation;
Area and perimeter of any polygon calculator will give the sum of interior angles, measures of interior and exterior angles, perimeter and area of the polygon.

Input: A positive integer as the number of sides of a regular polygon and a positive real number or parameter as the side length of a regular polygon;
Output: Five positive real numbers or variables as the sum of interior angles, measures of interior and exterior angles, perimeter and area of a regular polygon and corresponding units after that.

edges, center point and apothem of regular polygon

Polygon Formula

Perimeter of Regular Polygon Formula:
The perimeter, $P$, of a regular polygon is determined by the formula

$$P =\underset{n}{\underbrace{a+a+\ldots+a}}= n \times a$$

where $a$ is the side length and $n$ is the number of sides of the polygon.

Apothem of Regular Polygon Formula:
The apothem, $h$, of the regular polygon is determined by the formula

$$h=\frac{a}{2\times\tan \Big( \frac{180^o}{n}\Big)}$$

where $a$ is the side length and $n$ is the number of sides of the polygon.

Area of Regular Polygon Formula:
The area, $A$, of a regular polygon is determined by the formula

$$A=\frac {P\times h}2$$

where $P$ is the perimeter and $h$ is the apothem of the polygon.

Area of Regular Polygon Formula:
The area, $A$, of a regular polygon is determined by the formula

$$A=\frac {P\times a}{4\times\tan \Big( \frac{180^o}{n}\Big)}$$

where $a$ is the side length, $P$ is the perimeter and $n$ is the number of sides of the polygon.

What is Area & Perimeter of Polygon?

A closed figure bounded by line segments is the polygon. These segments are called its edges or sides, and the points where two sides meet are the polygon's vertices. For instance, in the following table are given some well-known polygons:

3	Triangle
4	Quadrilateral
5	Pentagon
6	Hexagon
7	Heptagon
8	Octagon
9	Nonagon
10	Decagon
12	Dodecagon
n	n-gon

Any polygon has both interior and exterior angles as shown in the picture below.

If we draw diagonals from one vertex in a $n$-gon, we divide it into $(n-2)$-triangles. Since the measure of interior angles in triangle is $180^o$, then the sum of the measures of the interior angles of a convex $n$-gon is $$(n-2)\times 180^o$$

The sum of the measures of the exterior angles of a convex $n$-gon is $360^o$.
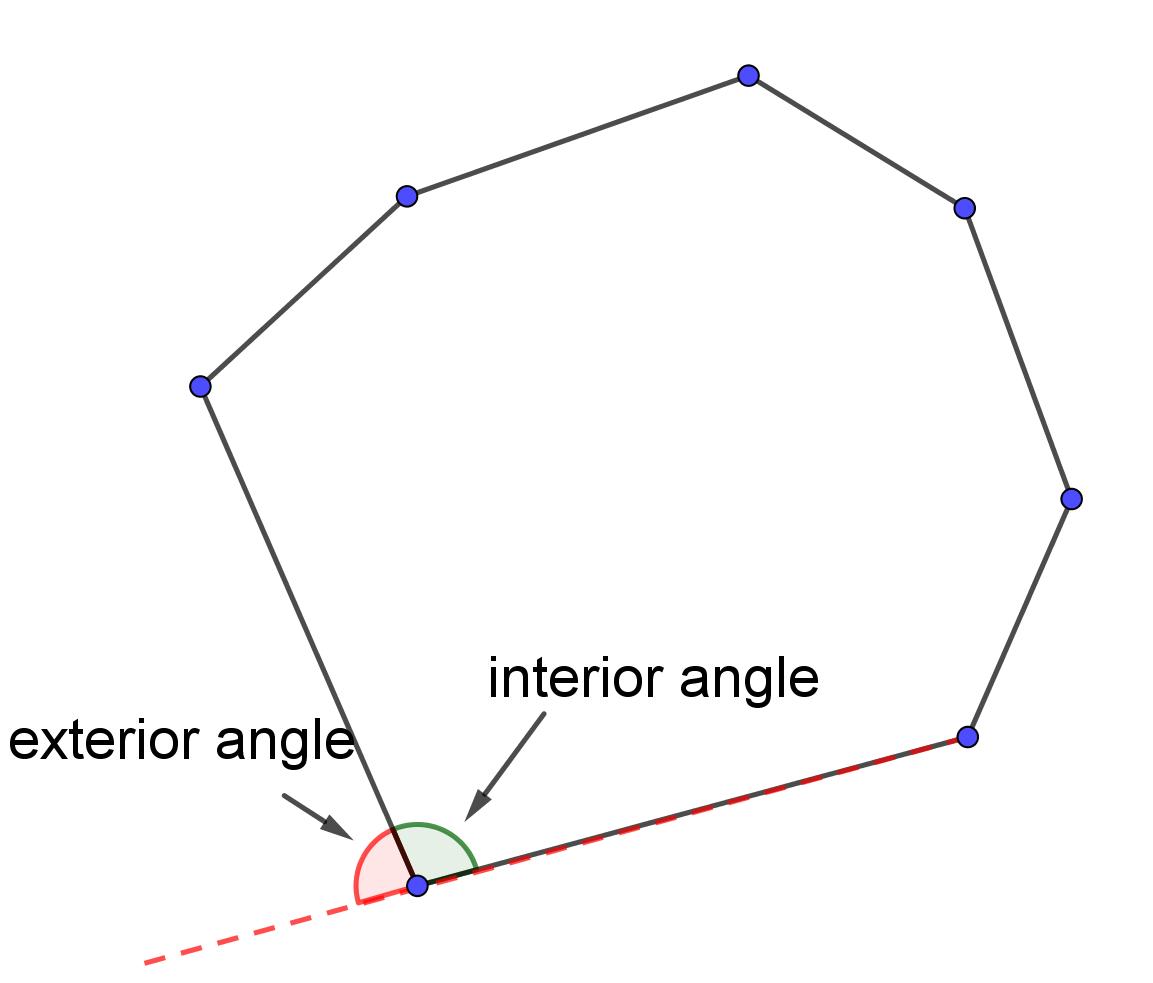
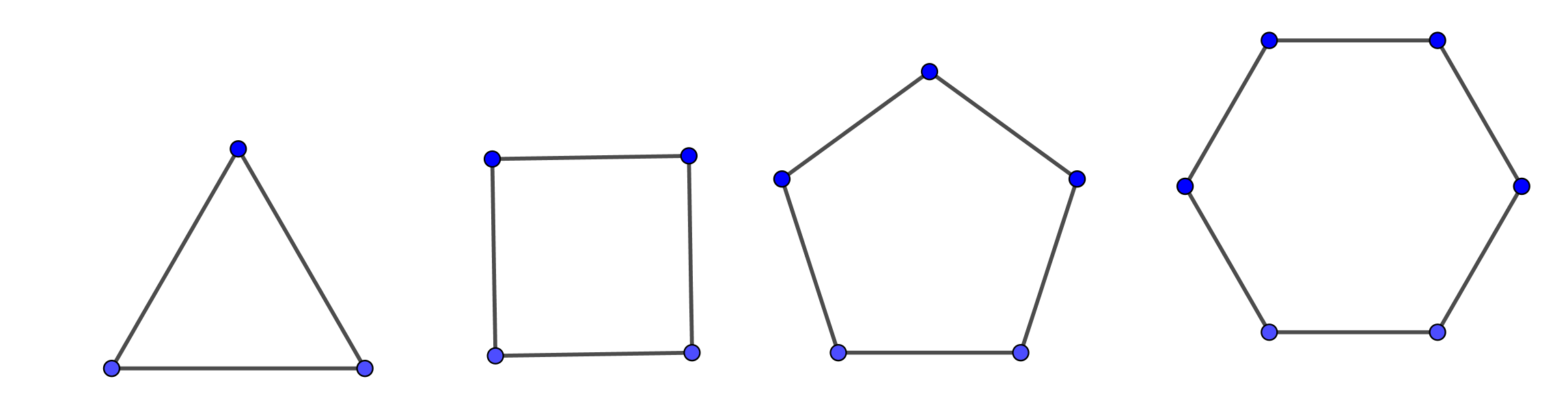
A polygon is a regular polygon if all its sides are congruent and all its angles are congruent. This means a regular polygon is a polygon that is both equiangular and equilateral. Equiangular polygon has all angles equal in measure, while equilateral polygon has all congruent sides. In the picture below are represented: equilateral triangle, square, regular pentagon, regular hexagon, respectively.

The regular polygon has the following properties:

Any regular polygon can be inscribed in a circle. The circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter;
Any regular polygon can be circumscribed in a circle. This means that any regular polygon has a incircle that is tangent to each side of the polygon at the midpoint;
A regular polygon can be constructed with compass and straightedge if and only if the odd prime factors of the number of sides are distinct Fermat primes. For instance, a regular pentagon can be constructed with compass and straightedge while a regular heptagon cannot be constructed with straightedge and compass;
Any regular polygon has rotational symmetry. Rotating a regular $n$-gon by a multiple of $\frac {360^o}n$ transforms the $n$-gon onto itself. For example, a regular octagon can be transformed onto itself by a clockwise or counterclockwise rotation of $45^o, 90^o, 135^o, 180^o,225^o, 270^o$, or $315^o$ about its circumcenter $O$.

Because of the sum of the measures of the interior angles of a convex $n$-gon is $(n-2)\times 180^o$, then the measure of each interior angle of a regular $n$-gon is

$$\frac{(n-2)\times 180^o}{n}$$

The measure of each exterior angle of a regular $n$-gon is

$$\frac{360^o}{n}$$

The distance around a polygon is called the perimeter of the polygon. It is usually denoted by $P$. To find the perimeter of a $n$-gon we add the lengths of its sides. Thus, the perimeter of a regular $n$-gon with the side length of $a$ is

$$P =\underset{n}{\underbrace{a+a+\ldots+a}}= n \times a$$

The area of a polygon, usually denoted by $A$, is a number of square units needed to fill the polygon. To find the formula for area of a regular $n$-gon, let us start with triangle. The area of any triangle with base length $a$ and height $h$ is

$$A = \frac {a\times h}2$$

Especially, the area of an equilateral triangle is one fourth the square of the length of the side times $\sqrt{3}$ i.e.

$$A=\frac{a^2\sqrt{3}}{4}$$

The distance from the circumcenter to any side of the regular polygon is called the apothem. For example the segment $\overline{OO'}$ is an apothem.

To find the area of any regular $n$-gon divide the polygon into congruent triangles. So, the area of any regular $n$-gon is

$$A=A(\Delta ABO)\times n=\frac {a\times h}2\times n=\frac {P\times h}2$$

To conclude, the area of a regular $n$-gon with side length $a$ is half the product of the apothem $h$ and the perimeter $P$.
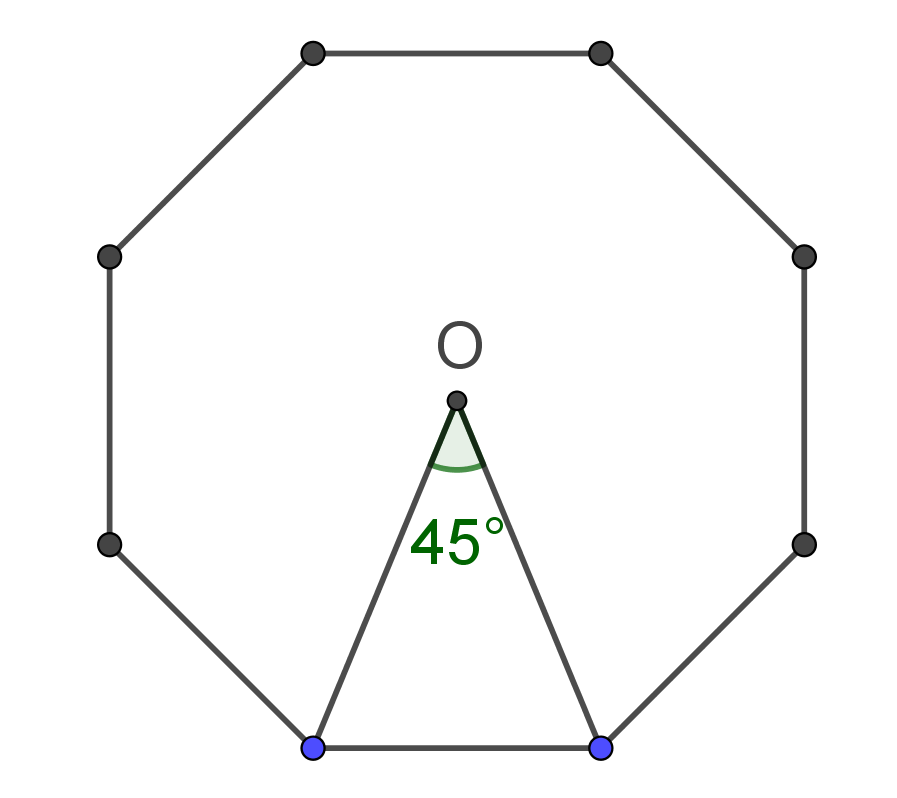
Since the central angle of a regular polygon is $\frac {360^o}n$, from the right triangle $\Delta OO'B$, the apothem can be calculated by the formula

$$h=\frac{a}{2\times\tan \Big( \frac{180^o}{n}\Big)}$$

Therefore, the area of a regular $n$-gon with side length $a$ is determined by the formula

$$A=\frac {P\times a}{4\times\tan \Big( \frac{180^o}{n}\Big)}$$

The perimeter is measured in units such as centimeters, meters, kilometers, inches, feet, yards, and miles. The area is measured in units such as square centimeters $(cm^2)$, square meters $(m^2)$, square kilometers $(km^2)$, etc.
For example, let us find the sum of interior angles, measures of interior and exterior angles, perimeter and area of a regular pentagon with the side length of $10$. The sum of interior angles of a pentagon is

$$(5-2)\times 180^o=3\times 180^o=540^o$$

The interior angle of a pentagon is

$$\frac {540^o}5=108^o$$

The exterior angle of a pentagon is

$$\frac {360^o}5=72^o$$

The perimeter of a pentagon with the side length of $10$ is

$$5\times 10=50$$

The area of a pentagon with the side length of $10$ is

$$A=\frac {50\times 10}{4\times\tan 36^o}\approx 172.0477 $$

The Area & Perimeter of any Polygon work with steps shows the complete step-by-step calculation for finding the sum of interior angles, measures of interior and exterior angles, perimeter and area of a regular pentagon with the side length of $10$ using the regular polygon formulas. For any other number of sides and the value of length of the side of a regular polygon, just supply a positive integer as the number of sides of a regular polygon and a positive real number or parameter as the side length of a regular polygon and click on the GENERATE WORK button. The grade school students may use this Area & Perimeter of any polygon calculator to generate the work, verify the results of geometry problems in the plane or do their homework problems efficiently.

Real World Problems Using Area & Perimeter of a Regular Polygon

Calculating areas and perimeters of regular polygons play an important role in almost all field of science and real life. A polyhedron is a solid whose surface consists of a number of polygonal faces. A polyhedron is regular if all its faces are congruent regular polygons and the same number of faces meet at every vertex. There are five convex regular polyhedra, known as the \underline{Platonic solids}: tetrahedron, cube, octahedron and dodecahedron, icosahedron. The surface area and volume of a regular polyhedron contain the formula for the area of regular polygon.

Tetrahedron, cube, octahedron, dodecahedron, icosahedron

Polygon Practice Problems

Practice Problem 1:
Find the area of regular dodecagon with lengths of sides and apothem of $14$ and $35$, respectively.

Practice Problem 2:
Find the number of sides and the measure of interior angles of a regular polygon if the measure of its exterior angle is $36^o$.

The polygon calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to understand the concept of perimeter and area of regular polygons. This concept can be of significance in geometry, to find the area and volume of some solids. Real life problems on regular polygons involving side length, measures of angles, apothem length, area, and perimeter are very common so these formulas can be of great the importance of solving.