Distance between Two Points Calculator
Dsiatnce between 2 Points - work with steps
Input Data :
Point 1`(x_A, y_A)` = (4, 3)
Point 2`(x_B, y_B)` = (3, -2)
Objective :
Find the distance between two given points on a line?
Formula :
Distance between two points = `\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}`
Solution :
Distance between two points = `\sqrt((3 - 4)^2 + (-2 - 3)^2)`
= `\sqrt((-1)^2 + (-5)^2)`
= `\sqrt(1 + 25)`
= `\sqrt(26)`
= 5.099
Distance between points (4, 3) and (3, -2) is 5.099
Distance between two points calculator uses coordinates of two points `A(x_A,y_A)` and `B(x_B,y_B)` in the two-dimensional Cartesian coordinate plane and find the length of the line segment `\overline{AB}`.
It’s an online Geometry tool requires coordinates of 2 points in the two-dimensional Cartesian coordinate plane.
It is necessary to follow the next steps:
- Enter coordinates (`x_A`,`y_A`) and (`x_B`,`y_B`) of two points `\text{A and B in the box}`. These values must be real numbers or parameters;
- Press the "GENERATE WORK" button to make the computation;
- Distance calculator will give the length of the line segment `overline{AB}`.
Output: A real number or variable
Distance Formula:

What is the Distance between Two Points?
For any two points there is exactly one line segment connecting them. The distance between two points is the length of the line segment connecting them. Note that the distance between two points is always positive. Segments that have equal length are called congruent segments.
| Distance between 2 Points | |
|---|---|
| (xA, yA) and (xB, yB) | Distance |
| (1, 2) and (3, 4) | 2.8284 |
| (1, 3) and (-2, 9) | 6.7082 |
| (1, 2) and (5, 5) | 5 |
| (1, 2) and (7, 6) | 7.2111 |
| (1, 1) and (7, -7) | 10 |
| (13, 2) and (7, 10) | 10 |
| (1, 3) and (5, 0) | 5 |
| (1, 3) and (5, 6) | 5 |
| (9, 6) and (2, 2) | 8.0623 |
| (5, 7) and (7, 7) | 2 |
| (8, 2) and (3, 8) | 7.8102 |
| (8, -3) and (4, -7) | 5.6569 |
| (8, 2) and (6, 1) | 2.2361 |
| (-6, 8) and (-3, 9) | 3.1623 |
| (7, 11) and (-1, 5) | 10 |
| (-6, 5) and (-3, 1) | 5 |
| (-6, 7) and (-1, 1) | 7.8102 |
| (5, -4) and (0, 8) | 13 |
| (5, -8) and (-3, 1) | 12.0416 |
| (-5, 4) and (2, 6) | 7.2801 |
| (4, 7) and ( 2, 2) | 5.3852 |
| (4, 2) and ( 8, 5) | 5 |
| (4, 6) and (3, 7) | 1.4142 |
| (-3, 7) and (8, 6) | 11.0454 |
| (-3, 4) and (5, 4) | 8 |
| (-3, 2) and (5, 8) | 10 |
| (-3, 4) and (1, 6) | 4.4721 |
| (-2, 4) and (3, 9) | 7.0711 |
| (-2, 4) and (4, 7) | 6.7082 |
| (-2, 5) and (5, 2) | 7.6158 |
| (-12, 1) and (12, -1) | 24.0832 |
| (-1, 5) and (0, 4) | 1.4142 |
| (-1, 4) and (4, 1) | 5.831 |
| (0, 1) and (4, 4) | 5 |
| (0, 5) and (12, 3) | 12.1655 |
| (0, 1) and (6, 3.5) | 6.5 |
| (0, 8) and (4, 5) | 5 |
| (0, 0) and (3, 4) | 5 |
| (0, 0) and (1, 1) | 1.4142 |
| (0, 1) and (4, 4) | 5 |
| (0, 5) and (12, 3) | 12.1655 |
| (2, 3) and (5, 7) | 5 |
| (2, 5) and (-4, 7) | 6.3246 |
| (2, 3) and (1, 7) | 4.1231 |
| (2, 8) and (5, 3) | 5.831 |
| (3, 2) and (-1, 4) | 4.4721 |
| (3, 12) and (14, 2) | 14.8661 |
| (3, 7) and (6, 5) | 3.6056 |
| (3, 4) and (0, 0) | 5 |
How to Calculate Distance between 2 Points?
The length of a segment is usually denoted by using the endpoints without an overline. For instance, the `\text{length of AB}` is denoted by `\overline{AB}` or sometimes `m\overline{AB}`. A ruler is commonly used to find the the distance between two points. If we place the `0` mark at the left endpoint, and the mark on which the other endpoint falls on is the distance between two points. In general, we do not need to measure from the 0 mark. By the ruler postulate, the distance between two points is the absolute value between the numbers shown on the ruler. On the other hand, if two points `A and B` are on the x-axis, i.e. the coordinates of `A and B` are `(x_A,0)` and `(x_B,0)` respectively, then the distance between two points `AB = |x_B −x_A|`. The same method can be applied to find the distance between two points on the y-axis. The formula for the distance between two points in two-dimensional Cartesian coordinate plane is based on the Pythagorean Theorem. So, the Pythagorean theorem is used for measuring the distance between any two points `A(x_A,y_A)` and `B(x_B,y_B)`
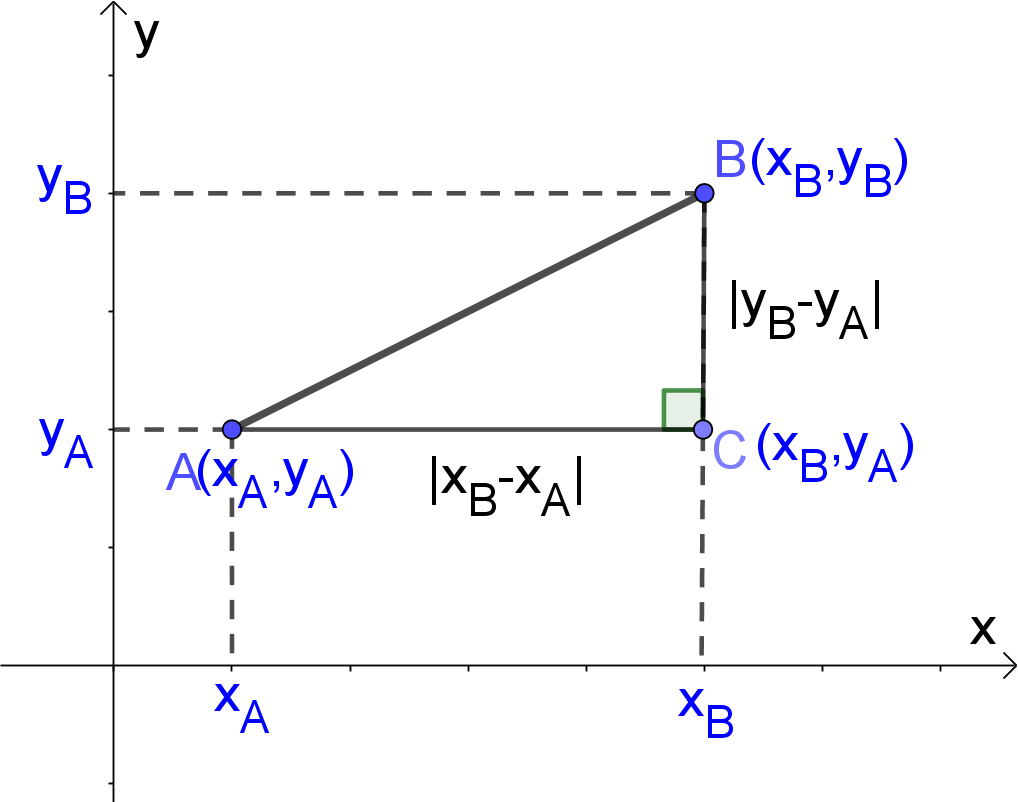
The distance can be also measured by using a scale on a map. The distance between 2 points work with steps shows the complete step-by-step calculation for finding a length of a line segment having 2 endpoints `A` at coordinates `(5,3)` and `B` at coordinates `(9,6)`. For any other combinations of endpoints, just supply the coordinates of 2 endpoints and click on the "GENERATE WORK" button. The grade school students may use this distance calculator to generate the work, verify the results or do their homework problems efficiently.
Real World Problems Using Length between Two Points
If we compare the lengths of two or more line segments, we use the formula for the distance between two points. We usually use the distance formula for finding the length of sides of polygons if we know coordinates of their vertices. In this case, we can explore the nature of polygons. It can also help us for finding the area and perimeter of polygon.
Length between two points calculator is used in almost all fields of mathematics. For example, the distance between two complex numbers `z_1 = a + ib` and `z_2 = c + id` in the complex plane is the distance between points `(a,b) and (c,d)`, i.e.
In physics, the length of the path between two points `A and B` during its motion is the distance. Based on the distance, some physical magnitudes can be defined. For example, speed is distance divided by time.
Distance between Two Points Practice Problems
Practice Problem 1:
Starting at the same point, Michael and Ann walked. Michael walked 5 miles north and 2 miles west, while Ann walked 7 miles east and 2 miles south. How far apart are them?
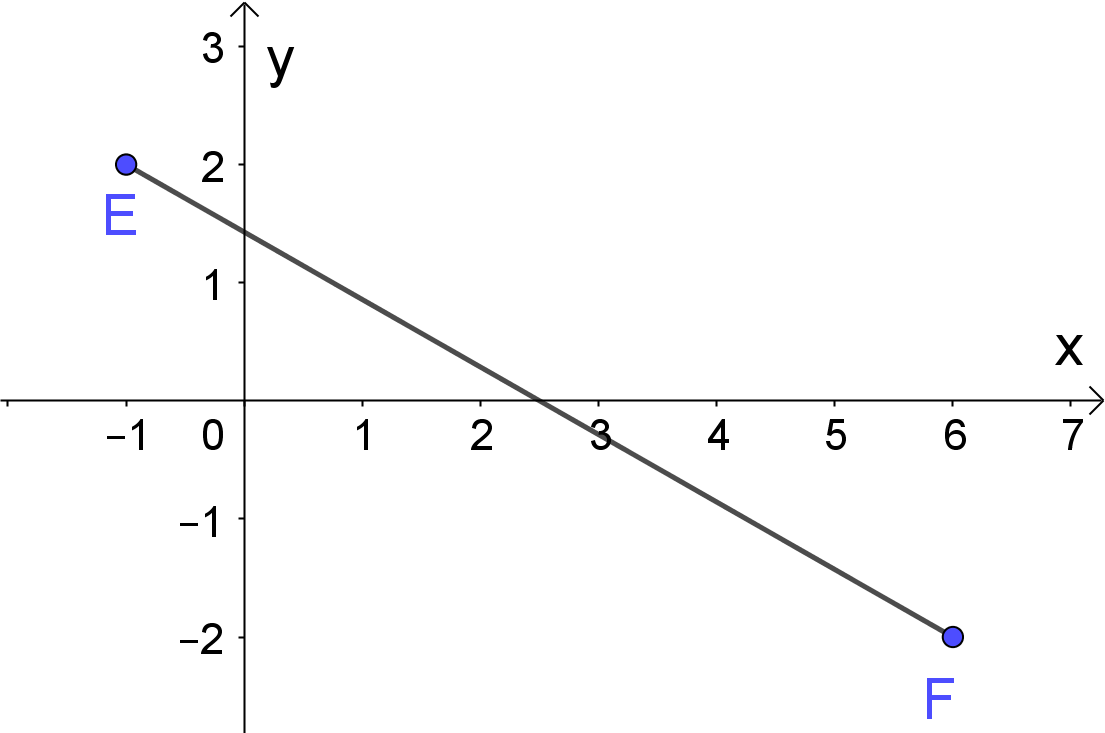
Practice Problem 2:
Find the distance between points `E and F.`
The distance calculator, formula, example calculation (work with steps) and practice problems would be very useful for grade school students (K-12 education) to learn what is distance between two points in geometry, how to find it and where it can be applicable in real world problems.
