Perpendicular Distance Calculator
Perpendicular Distance - work with steps
Input Data :
Coordinates 1 (x1, y1) = (2, 3)
Equation Ax+by+c = 8x + 7y + 5
Objective :
Find what is the length of perpendicular distance?
Formula :
Perpendicular Distance = (Ax1 + By1 + C)√(A2 + B2)
Solution :
Perpendicular Distance = 8(2) + 7(3) + 5√((8)2
+ (7)2)
= 16 + 21 + 5√(64
+ 49)
= 42√(113)
= 4210.6301
Perpendicular Distance = 3.951
perpendicular distance calculator - step by step calculation, formula & solved example to calculate the distance from a point or coordinates (x1, y1) to line Ax + By + C = 0 in a two dimensional space or XY plane. x1, y1 is the point and the Ax + By + C = 0 is the line in the two dimensional space or XY plane.
Formula
The below formula is used to find the perpendicular length from a point to a line.
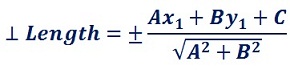
Solved Example
This below solved example let users to understand how the example values are being used in this calculation to determine perpendicular length from a point to line.
Problem:
Find the perpendicular distance from the point (5, 6) to a line 7x + 9y + 12 = 0.
Solution:
Let's consider x1 = 5 & y1 = 6
Apply the values in the formula
= ((7 x 5) + (9 x 6) + 12) / √(72 + 92)
= 101/√(130)
Perpendicular Length = 8.8583
Unlike most of the other calculators online, this featured geometry tool provides the complete step by step calculation for every calculations user do by using this perpendicular length calculator. This calculator along with formula & solved example calculation let users to understand, practice & verify such calculations.
