Arithmetic Progression Calculator

Number of Terms

First Term

Difference

`n^{th}` Term (`T_n`) = 100

`n^{th}` Partial Sum (`S_n`) = 5050

GENERATE WORK

CALCULATE

Arithmetic Progression - work with steps

Input Data :
Number of Terms (`n`) = 100
First Term (`a`) = 1
Difference (`d`) = 1

Objective :
Find `n^{th}` term and `n^{th}` partial sum of an arithmetic sequence?

Formula :
`n^{th}` Term (`T_n`) `= a + (n - 1)d`
`n^{th}` Partial Sum (`S_n`) `= n/2(a + T_n)`

Solution :
`n^{th}` Term (`T_n`) = 1 + (100- 1)1
= 1 + (99) x 1
= 1 + 99
`T_n` = 100

`n^{th}` Partial Sum (`S_n`)` = 100/2 (1 + 100)`

` = 100/2 \times101`

` = 10100/2`
`S_n` = 5050

Arithmetic progression calculator calculates the `n^(th)` term and the `n^(th)` partial sum of an arithmetic progression.
It is necessary to follow the next steps:

Enter the number of terms of an arithmetic progression in the box. This value must be positive integer. Enter the first term and the common difference in the box. The first term can be a real number or variable, and the common difference must be real number;
Press the "GENERATE WORK" button to make the computation;
Arithmetic progression calculator will give nth term and the nth partial sum of an arithmetic progression.

Input: There are three inputs: the number of terms, the first term, and the common difference of an arithmetic progression. The number of terms must be positive integer, the first term can be in terms of real numbers or variables, and the common difference must be real number
Output: The outputs (the `n^(th)` term and the sum of n terms of the arithmetic progression ) are in terms of real numbers of variables.

`n^(th)` term of an arithmetic progression:

Explicit Formula: The `n^(th)` term of an arithmetic progression `(a_n)_(n∈N)` is

$$a_n =a_1+(n-1)d,$$

where d is the common difference and a1 is the initial term of the arithmetic progression.
Recurrent Formula: The `n^(th)` term of an arithmetic progression (a_n)_n∈N is

$$a_n =a_{n-1}+d,$$,

where d is the common difference and an−1 is the `(n − 1)^(th)` term of the arithmetic progression.

Formula for the nth partial sum of an arithmetic progression:

There are two equivalent formulas for the sum of the first n terms of an arithmetic progression `(a_(n))_(n∈N)` :

$$S_n=\frac{n}{2} \big[2a_1+(n-1)d\big]$$

$$S_n=\frac{n}{2} (a_1+a_n),$$

where `a_(1)` and `a_(n)` are is the initial and the last term of the arithmetic progression, respectively, and `n` number of terms in the arithmetic progression.

What is Arithmetic Progression?

A progression is a function with positive integers as its domain. The terms of a progression belong to the range of the function. The first term of a progression is usually denoted by `a_1`, the second term by `a_2`, and so on up, the nth term by an. A progression `(a_(n))_(n∈N)` such that each term is obtained from the preceding one by adding a constant is an arithmetic progression or an arithmetic sequence. In other words, any arithmetic progression has the form

$$a_1, a_1+d, a_1+2d, a_1+3d, a_1+4d,\ldots$$

where the constant d is the common difference. The first term `a_1` is called the initial term. Note that the common difference d can be positive, negative or zero

If the common difference is positive, d > 0, then the arithmetic progression is an increasing progression and it holds

a₁ <a₂< . . .<a_{n-1}<a_n
If the common difference is positive, d < 0, then the arithmetic progression is an decreasing progression and it holds

$$a_1>a_2>\ldots>a_{n-1}>a_n$$
The constant progression is only progression that is both arithmetic and geometric.

If each term of an arithmetic progression is increased, decreased, multiplied, or divided by a non-zero number, then the resulting progression is also arithmetic progression.

The terms between two nonconsecutive terms of an arithmetic progression `(a_(n))_(n∈N)` are called arithmetic means of these terms. For example, the arithmetic means between `a_1` and `a_6` are `a_2`, `a_3`, `a_4` and `a_5`. When two nonconsecutive terms of an arithmetic progression `(a_n)_n∈N` are given and we know the number of arithmetic means between them, then we can fully determine this progression.

A series is a sum of the terms of an arithmetic progression. A series can be infinite or finite. The `n^(th)` partial sum, usually denoted by the symbol `S_n`, represents the sum of the first `n` terms of a series.

How to Calculate nth Term or Sum of n Terms of Arithmetic Progression?

In the problems which require to find the next term in an arithmetic progression, first we find the common difference by subtracting any term from its succeeding term, then we add the common difference to the last term. For instance, the `n^(th)` term `a_n` is equal to $a_{n-1}+d$, where `a_(n−1)` is the `(n − 1)^(th)` term. Therefore,

$$a_n=a_{n-1}+d$$

This formula is well know as a recursive formula.

If we follow this procedure and recursive formula, the `(n−1)^(th)` term `a_(n−1)` is equal to `a_{n-3}+d`, where `a_(n−2)` is the `(n − 2)^(th)` term, the `(n − 2)^(th)` term `a_(n−2)` is equal to `a_(n−3) + d`, where `a_(n−3)` is the `(n − 3)^(th)` term, etc. After `(n − 1)` iterations, we get the formula for the nth term of an arithmetic progression

$$a_n=a_{n-1}+d=a_{n-2}+d+d=\ldots=a_{1}+\underset{n-1}{\underbrace{d+d+\ldots+d}}=a_1+(n-1)d$$

Hence, the `n^(th)` term of an arithmetic progression can also be determined from the first term and the common difference. From the exposed above, any two terms `a_n` and `a_m` `(n > m)` of an arithmetic progression `(a_n)_(n∈N)` satisfy the following relation

$$a_n=a_m+(n-m)d$$

In developing a formula for the `n^{th}` partial sum for a finite arithmetic series, a series can be written in the following way

$$S_n=a_1+(a_1+d)+(a_1+2d)+\ldots+(a_1+(n-1)d)$$

So,

$$S_n=na_1+[1+2+3+\ldots+(n-1)]d$$

Since the sum of the first `(n-1)` positive integers is `\frac{(n-1)n}{2}`, by substituting this results in the previous formula, we obtain

`S_n=na_1+\frac{(n-1)n}{2}d` `= \frac{n}{2}[2a_1+(n-1)d]`

When the value of the last term an is known, then using the formula for the `n^{th}` term of an arithmetic progression, `a_n = a_1 + (n − 1)d`, we can derive another formula for the nth partial sum of an arithmetic progression:

$$S_n=\frac{n}{2} (a_1+a_n)$$

Arithmetic progression calculator work with steps shows the complete step-by-step calculation for finding the `n^{th}` term and the `n^{th}` partial sum of an arithmetic progression such that there is `5` terms in the arithmetic progression, the first term is `5`, and the common difference is `4`. For any other combinations the number of terms, the first term, and the common difference, just supply the other numbers as inputs and click on the on the "GENERATE WORK" button. The grade school students may use this arithmetic progression calculator to generate the work, verify the results or do their homework problems efficiently.

Sum of First n Numbers
Sum of first 100 natural numbers	5050
Sum of first 50 even numbers	2550
Sum of first 50 odd numbers	2500
Sum of first 50 natural numbers	1275
Sum of first 100 odd numbers	10000
Sum of first 100 even numbers	10100
Sum of first 10 numbers	55
Sum of first 10 odd numbers	100
Sum of first 10 even numbers	110
Sum of first 25 natural numbers	325
Sum of natual numbers from 51 to 100	3775
Sum of natual numbers from 50 to 100	3825
Sum of natual numbers from 20 to 50	1085

Real World Problems Using Arithmetic Progression

Arithmetic progressions are very important in mathematics. They have many useful applications in physics, statistics, finance, etc.

In working with linear functions, when we increase the `x`-value by `1` unit, the `y`-value increases by a fixed number, equal to the slope. The next term in an arithmetic progression is derived by adding the common difference to the last term. So, arithmetic progressions are something like linear functions, with the common difference as the slope.

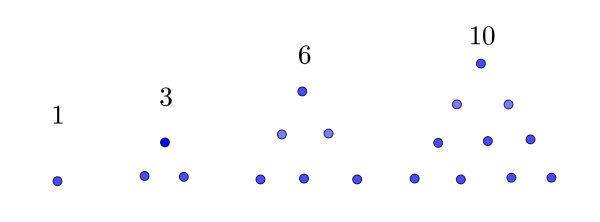
The partial sum of an arithmetic progression has an application in the theory of numbers. For instance, the triangular numbers are the sums of the consecutive positive integers.The first triangular number is `1`, the second is the sum of `1+2=3`, the third is `1+2+3=6`, the fourth is `1+2+3+4=10` and so on. The sequence of the triangular numbers is the sequence of the partial sums of the arithmetic sequence `1,2,3,4\ldots`

Arithmetic Progression Practice Problems

Practice Problem 1:
We have `\$1000` and go to the bank to deposit money. The bank gives us the following option: the first month we receive `\$1000`, the second month we receive `\$1080`, the third month we receive `\$1160`, etc. How much money will we receive after `15` months?

Practice Problem 2:
Given the sequence by the recurrence relation `a_{n+1} = a_n − 5` and `a_1 = 10`. Find the sum of the first `15` terms of the arithmetic sequence.

The arithmetic progression calculator, formulas for the `n^{th}` term of the sequence and the sum of `n` numbers of the sequence, step by step calculation and practice problems would be very useful for grade school students (K-12 education) in studying series and sequences and in solving real world problems.