Prime Factorization Calculator

Prime Factors of a Number calculator finds all prime factors of a positive integer. For small numbers we can calculate the prime factors simply. When it comes to large numbers, finding out the prime factors may be time consuming and bit complicated. To make calculations easy, this calculator will help us to figure out all the prime factors of the given number.
It is necessary to follow the next steps:

1. Enter a number in the box. The number must be positive integer;
2. Press the "CALCULATE" button to make the computation;
3. Prime factors of a number calculator will give all prime factors of the entered number.

Input : A positive integer;
Output : List of prime numbers.

What is Prime Factors?

The prime factors are the smaller integers found by decomposing the composite number into prime numbers. The product of prime factors forms any positive integer. A prime number is a natural number greater than $1$ that has exactly two factors, $1$ and itself. Negative integers cannot be prime. A composite number is any positive integer that is not prime. Zero and 1 are neither prime nor composite numbers. For example

How to Find Prime Factorization of a Number?

The prime factors of a number can be found by factor tree. A factor tree is a special diagram for finding the factors of a composite number, until getting all prime factors. For example, let us find the prime factor of `20` by using the factor tree:

As we can see, both trees give the same prime factors. There is exactly one prime factorization of `20`. The prime factors of `20` is $$20=2\times2\times 5=2^2\times5$$ The fundamental theorem of arithmetic states that every integer greater than $1$ can be factored uniquely into primes (Hardy, G. H., and Wright, E. M., An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 3 and 21, 1979.). For instance, $20$ can be factored uniquely into $2\times2\times5$, i.e. there is no other product of primes equal to `20`.
Another method for finding the factors of a composite number is called the cake method. To find the prime factors of a composite number, we need to follow the next steps:

• Divide a composite number by its smallest factor;
• Divide a quotient number by its smallest factor;
• Repeat the previous step until the quotient is prime;
• The prime factors are listed.

For example, let us find the the prime factors of `468` by using the cake method So, the prime factorization of
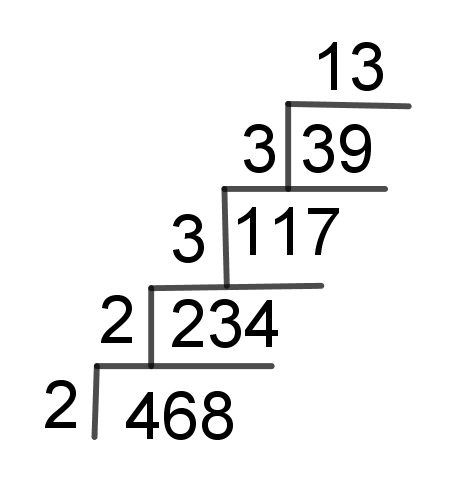
A monomial can also be factored as a product of prime numbers and variables with no exponent greater than $1$. Negative coefficients can be factored using $-1$ as a factor. For example, the factors of monomials $12xy^2$ are $12xy^2=2\times2\times3\times x\times y\times y$.

Real World Problems Using Prime Factors

The prime factorization is used in finding the greatest common factor (GFC) and least common multiple (LCM) of two or more numbers. In fraction addition, the LCM is one of the important things. The GCF is useful for simplifying fractions, etc. The prime factorization is of great interest in number theory and application. For instance, the prime factorization is also the essence of Chinese remainder theorem of solving simultaneous congruent equations.

Practice Problem 1:
Find the prime factors of `125`.

Practice Problem 2:
Using the prime factorization find the smallest integer number $n$ such that `1960n` is a cube number.

The Prime factors of a number calculator, methods, example calculation and practice problems would be very useful for grade school students of K-12 education to learn how to find the prime factorization of a given number. They can use this concept to find the GFC and LCM of a given set of numbers, monomials and polynomials.