Percentage Calculator
Percentage - work with steps
Input Data :
X = 10
Y = 500
Objective :
Find what is 10% of 500?
Formula
X% of Y `= (X /100) \times Y`
Solution :
X% of Y `= (10 /100) \times 500`
= 0.1 x 500
X percent of Y = 50
Percentage calculator uses the values of $X$, $Y$ and calculate the $X$ percent of $Y$. It is an online Algebra tool requires two numbers $X$ and $Y$ and find $X\%$ of $Y$.
It is necessary to follow the next steps:
- Enter values for the $X$ percent and the base $Y$ in the box. The value of $X$ must be positive real number and the value of $Y$ must be real number or parameter;
- Press the "GENERATE WORK" button to make the computation;
- Percentage calculator will give the $X\%$ of $Y$.
Output : A real number or variable.
$X$ percent of $Y$ Formula:
What is $X$ percent of $Y$?
The word "percent", originally "per centum", means "by the hundred". It is a ratio which compares a number to hundred. Percent deals with the fractions whose denominators are $100$. These fractions can be written also as decimals. The symbol $\%$ is placed after the number. For example, $25\%$ represents $\frac{25}{100}$ or $0.25$.
In changing decimal to percent or vice-versa, we need to follow the next procedures:
- To write a percent as a decimal, divide it by $100$ and remove the percent symbol;
- To write a decimal as a percent, multiply it by $100$ and add the percent symbol.
A percent may be greater than $100\%$ or less than $1\%$. Whole numbers are the special types of percents that are greater than $100\%$. For example, the number $5$, in terms of percent is $500\%$. Percents larger than $100\%$ can be transformed to decimals by the same procedure as ordinary percents. For example, $325\%$ is equivalent to $3.25$. A fractional percent represents a percent less than $1\%$. In this case, it is easier to find $1$ percent of the number and then find the fractional part.
In a percent proportion, one of the numbers is called the part and it is compared to the whole magnitude, named the base. The other ratio is the percent, which base is $100$. Therefore,
A changes in quantities can be represented through percents. A percent of change is increased or decreased the percent an amount in relation to the original amount. The formula for the percent change is
A percent difference between two numbers $Y_1$ and $Y_2$ is the absolute value of the difference between two numbers, divided by the average of these numbers, and multiplied by $100\%$. This means,
How to calculate $X$ percent of $Y$?
To determine $X$ percent of a real number $Y$, change the percent to a fraction or decimal and multiply it by $Y$. The word "of" means multiply.
The percentage work with steps shows the complete step-by-step calculation for finding $X$ percent of $Y$ with the percent $X=10$ and the base $Y=500$. For any other combinations of the percent $X$ and the base $Y$, just supply values of the percent and the base and click on the "GENERATE WORK" button. The grade school students may use this percentage calculator to generate the work, calculate the percentage of marks, represent numbers as percents, verify the results or do their homework problems efficiently.
Real World Problems Using $X$ percent of $Y$
Percentage can be used in different fields of life and science. For example, in accounting and finance the percentage is used in finding interest rates, sales and taxes. The prices of most items increase or decrease by a percentage. By the percentage, we can express the average grades of the students and also we can analyze or compare some progress. Pie Charts, are a very commonly used to describe the proportions of a given data set in terms of percentages or fractions. For example, if the circle is divided by the corresponding central angles, then the area of the red part is $\frac{144}{360}=40\%$ of whole. Conversely, in order to find the measure of the central angle, we have to find the percent represented by the piece, then multiply $360^o$ by the percent.
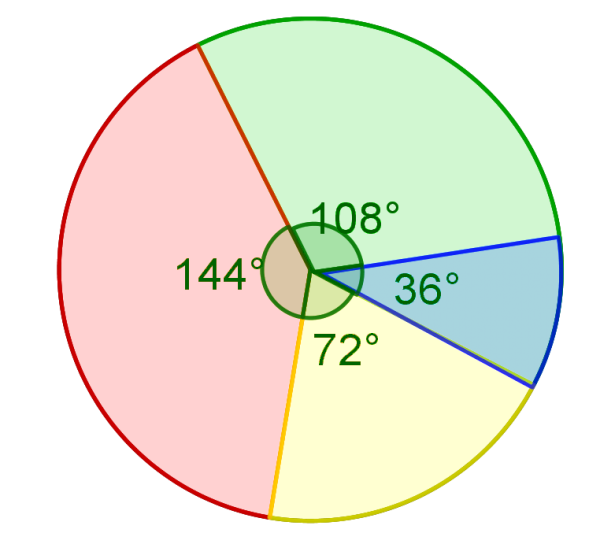
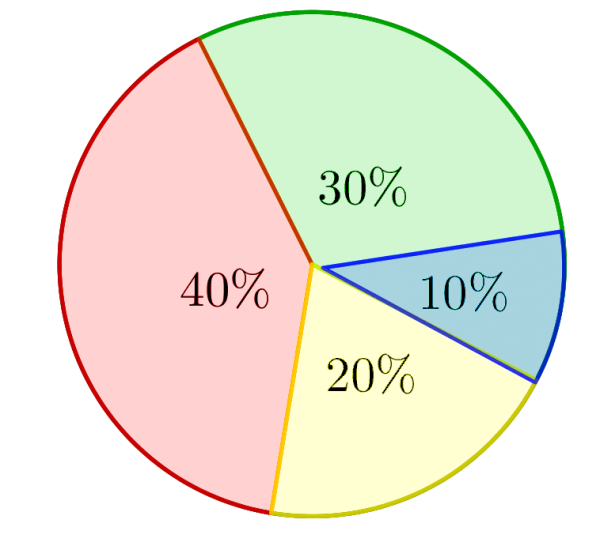
Percentage Practice Problems
Practice Problem 1:
Find the $16\%$ of $\$186$.
Practice Problem 2:
A pizza is on sale at a $12.5\%$ discount. Find the new price the pizza, if the original price of the pizza is $\$15.$
Practice Problem 3:
France has a sales tax of $19.6$ percent. If we purchased a car for $\$25,000$, how much would we pay for the car if we bought it in France?
The percentage calculator, formula, example calculation (work with steps), real world problems and practice problems would be very useful for grade school students (K-12 education) to learn how to find percent of some numbers. This concept is very useful in real-life, for instance, to solve problems based on discount and markup.
