Linear Regression Calculator

Dataset set x

comma separated input values

Dataset set y

comma separated input values

Number of samples = 5

X mean = 6.4

Y mean = 14.6

Slope(B) = 4.0943

Intercept = 1.6415

Regression equation = 1.6415 + 4.0943 x

GENERATE WORK

CALCULATE

Linear Regression - work with steps

Input Data :
Data set x = 4, 5, 6, 7, 10
Data set y = 3, 8, 20, 30, 12
Total number of elements = 5

Objective :
Find what is the linear relationship between two datsset X and Y?

Solution :
X_mean = (4 + 5 + 6 + 7 + 10)/5
= 32/5
X_mean = 6.4

Y_mean = (3 + 8 + 20 + 30 + 12)/5
= 73/5
Y_mean = 14.6

Slope = (∑y)(∑x²) - (∑x)(∑xy)n(∑x²) - (∑x)²
∑y = 3 + 8 + 20 + 30 + 12
∑y = 73
∑x² = (4)² + ( 5)² + ( 6)² + ( 7)² + ( 10)²
= 16 + 25 + 36 + 49 + 100
∑x² = 226
∑x = 4 + 5 + 6 + 7 + 10
∑x = 32
∑xy = (4 x 3) + ( 5 x 8) + ( 6 x 20) + ( 7 x 30) + ( 10 x 12)
∑xy = 12 + 40 + 120 + 210 + 120
∑xy = 502
Apply the values in above formula
Slope = (73 x 226) - (32 x 502))(5 x 226) - (32)²
= 16498 - 160641130 - 1024
= 434106
Slope = 4.0943

Intercept = n(∑xy) - (∑x)(∑y)n(∑x²) - (∑x)²
= 5(502) - (32 x 73)(5 x 226) - (32)²
= 2510 - 23361130 - 1024
= 174106
Intercept = 1.6415

Regression equation = Intercept + Slope x
Regression equation = 1.6415 + 4.0943 x

Linear Regression calculator uses the least squares method to find the line of best fit for a sets of data `X` and `Y` or the linear relationship between two dataset. It estimates the value of a dependent variable `Y` from a given independent variable `X`. It's an online statistics and probability tool requires two sets of data `X` and `Y` and finds the relationship between two variables by fitting a linear equation to observed data.
It is necessary to follow the next steps:

Enter two data sets `X` and `Y` (observed values) in the box. These values must be real numbers or variables and may be separated by commas. The number of values should be the same for `X` and `Y`. The values can be copied from a text document or a spreadsheet.
Press the "GENERATE WORK" button to make the computation.
Linear regression calculator will find the relationship among variables `X` and `Y`.

Input : Two lists of real numbers separated by comma;
Output : A linear function $\hat {y}=a+bx$.

Linear regression calculator gives us the stepwise procedure and insight into every step of the calculation. Before the final result of the linear regression line is derived, it calculates the sample means of two sets of data. These values of the sample means can be of benefit for further solving of problems and applications.

Linear Regression Line Formula:

For two data sets $X=(x_1,\ldots, x_n)$ and $Y=(y_1,\ldots,y_n)$, coefficients `a` and $b$ of the linear regression line, $\hat {y}=a+bx$, are determined by the following equations:

$$\begin{align} a&=\frac{(y_1+ \ldots+y_n )(x_1^2+ \ldots+x_n^2 )-(x_1+\ldots +x_n)(x_1 y_1+ \ldots+x_n y_n)}{n(x_1^2+ \ldots+x_n^2 )-(x_1+ \ldots+x_n )^2},\\ b&=\frac{n(x_1 y_1+ \ldots+x_n y_n )-(x_1+\ldots+x_n)(y_1+\ldots+y_n)}{n(x_1^2+ \ldots+x_n^2 )-(x_1+ \ldots+x_n )^2 }\end{align}$$

What is Linear Regression?

Linear regression is a model of the relationship between a dependent variable `y` and independent variables `x` by linear prediction function $\hat {y}=a+bx$. Linear functions are used to model the data in linear regression and the unknown model parameters are estimated from the data. Such method of modeling data is known as linear models. For more two or more variables, this modeling is called multiple linear regression. Linear regression models are often fitted using the least squares regression line. The least squares regression line is the line $\hat {y}=a+bx$ that makes the vertical distance from the data points to the regression line as small as possible. We call it "least squares" because the best line of fit is one that minimizes the sum of squares of the errors. So, the line of best fit is the least squares regression line $\hat {y}=a+bx$, where $b$ is the slope of the line and `a` is the `Y`-intercept.

How to Find Linear Regression?

Let us consider two samples $X=(x_1,\ldots,x_n)$ and $Y=(y_1,\ldots, y_n)$ of `n` outcomes. Coefficients `a` and `b` of the least squares regression line, $\hat {y}=a+bx$, can be determined from the equations:

If we know the equation of least squares regression line from some data, we can use it to predict the `y`-value for a given `x`-value. The slope of the regression line is the predicted change in the `y`-value when the `X`-value increases by `1`.
The least squares regression line can be found in the other way. Let $\bar X$ and $\bar Y$ be the corresponding sample means and `s_X` and `s_Y` be sample deviations of these variables. The least squares regression line is the line $\hat {y}=a+bx$ for $$b=s_{XY} \frac{s_Y}{s_X},\quad a=\bar Y -b\bar X$$ and correlation coefficient $r_{XY}$ between `X` and `Y`.
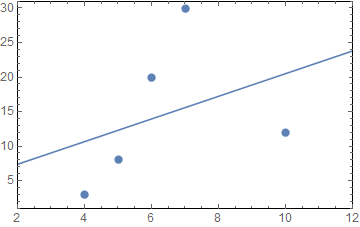
For example, for data sets $X:4,5,6,7,10$ and $Y:3,8,20,30,12$, we obtain

$\begin{align} a&=\frac{(3+8+20+30+12)(4^2+5^2+6^2+7^2+10^2)-(4+5+6+7+10)(4\cdot3+5\cdot 8+6\cdot 20+7\cdot 30+10\cdot 12)}{5(4^2+5^2+6^2+7^2+10^2)-(4+5+6+7+10)^2}\\ &=\frac{73\cdot 226-32\cdot 502}{1130-1024}\\ &=\frac{217}{53}=4.09434\\ b&=\frac{5(4\cdot3+5\cdot 8+6\cdot 20+7\cdot 30+10\cdot 12)-(4+5+6+7+10)(3+8+20+30+12)}{5(4^2+5^2+6^2+7^2+10^2)-(4+5+6+7+10)^2 }\\ &=\frac{5\cdot502-32\cdot 73}{1130-1024}\\ &=\frac{87}{53}=1.64151\end{align}$

So, the line $y= 4.09434+1.64151x$ is the regression line. A scatter plot is used to show a relationship between these two variables and linear regression line is used to fit a model between the two variables.

The Linear Regression work with steps shows the complete step-by-step calculation for finding the covariance of the two samples $X:4,5,6,7,10$ and $Y:3,8,20,30,12$. For any other samples, just supply two lists of numbers and click on the "GENERATE WORK" button. The grade school students may use this linear regression calculator to generate the work, verify the results derived by hand or do their homework problems efficiently.

Linear Regression Practice Problems

Linear regression has many applications. If the goal is a prediction, linear regression can be used to fit a predictive model to a data set of values of the response and explanatory variables. Linear regression can help in analyzing the impact of varied factors on business sales and profits. For example, predictive analytics, operation efficiency, correcting errors, etc. By using this concept, we can analyze the marketing effectiveness, pricing, and promotions on sales of a product.
Also, linear regression can be useful in studying engine performance from test data in automobiles, to model causal relationships between parameters in biological systems, and in many other fields of science and life.

Practice Problem 1:
Mitchell is the basketball player. The number of minutes in games `X` and the numbers of points `Y` are in the table below

G1	G2	G3	G4	G5	G6	G7
26	38	19	36	38	12	24
12	15	9	26	34	5	15

Find the least squares regression line of this data.

Practice Problem 2 :
At the Mathematics Department, students took an examination in algebra and geometry in the last week. The numbers of students who passed the exams are given in the following table

	Monday	Tuesday	Wednesday	Thursday	Friday	Saturday	Sunday
Geometry	14	18	19	36	18	2	14
Algebra	24	45	19	16	14	5	16

Find the least squares regression line of this data.

The linear regression calculator, formula, work with steps, rela world problems and practice problems would be very useful for grade school students (K-12 education) to learn what is linear regression in statistics and probability, and how to find the line of best fit for two variables. Students can apply this concept to ANCOVA (analysis of covariance) to compare regression lines by testing the effect of a categorical value on a dependent variable.