Skewness Calculator
Skewness Calculator - work with steps
Input Data :
Data set = 3, 8, 10, 17, 24, 27
Total number of elements = 6
Objective :
Find what is skewness for given input data?
Formula :
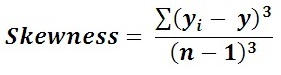
Solution :
mean = (3 + 8 + 10 + 17 + 24 + 27)/6
= 89/6
ymean = 14.8333
sd = √(1/6 - 1) x ((3 - 14.8333)2 + ( 8 - 14.8333)2 + ( 10 - 14.8333)2 + ( 17 - 14.8333)2 + ( 24 - 14.8333)2 + ( 27 - 14.8333)2)
= √(1/5) x ((-11.8333)2 + (-6.8333)2 + (-4.8333)2 + (2.1667)2 + (9.1667)2 + (12.1667)2)
= √(0.2) x ((140.027) + (46.694) + (23.3608) + (4.6946) + (84.0284) + (148.0286))
= √(0.2) x 446.8333
= √89.3667
sd = 9.4534
Skewness = ∑(yi - ymean)(n - 1) x (sd)³
= (3 - 14.8333)³ + ( 8 - 14.8333)³ + ( 10 - 14.8333)³ + ( 17 - 14.8333)³ + ( 24 - 14.8333)³ + ( 27 - 14.8333)³(6 - 1)³ x 9.4534
= (-11.8333)³ + (-6.8333)³ + (-4.8333)³ + (2.1667)³ + (9.1667)³ + (12.1667)³(5)³ x 9.4534
= (-1656.9814) + (-319.074) + (-112.9097) + (10.1718) + (770.263) + (1801.0194)125 x 9.4534
= 492.48911181.675
Skewness = 0.1166
Skewness Calculator is an online statistics tool for data analysis programmed to find out the asymmetry of the probability distribution of a real-valued random variable. This calculation computes the output values of skewness, mean and standard deviation according to the input values of data set.
Definition
Skewness is an asymmetry measure of probability distribution of a real valued random variable. The value of skewness can be positive or negative, or even undefined. A negative skew specifies that the tail on the left side of the probability density function is longer than the right side and the size of the values probably including the median lie to the right of the mean. A positive skew specifies that the tail on the right side is longer than the left side and the size of the values lie to the left of the mean. A zero value indicates that the values are relatively constantly distributed on both sides of the mean, usually but not necessarily involving a symmetric distribution.
How to Calculate Skewness
1. Calculate the mean and standard deviation
2. Subtract the mean from each raw score
3. Raise each of these deviations from the mean to the third power and sum
4. Calculate skewness, which is the sum of the deviations from the mean, raise to the third power, divided by number of cases minus 1, times the standard deviation raised to the third power.
The Formula for Skewness Calculation
The term Skewness in Probability theory or Statistics, can be derived from the formula
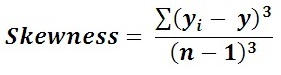
The collection of tools employs the study of methods and procedures used for gathering, organizing, and analyzing data to understand theory of Probability and Statistics. The set of ideas which is intended to offer the way for making scientific implication from such resulting summarized data. The above illustrations can guide you to understand how to find out the Skewness in statistics. There may be occasion arises when you need to find out the Skewness value for large set of data where use this online Skewness calculator to precisely determine the value to the given set of numbers or data
