Z-Score Calculator
Standardized or Z-Score - work with steps
Input Data :
Random Value (X) = 9.25
Mean (μ) = 9
Standard Deviation (σ) = 0.73
Objective :
Find what is the normalized score of random member X?
Formula :
z-score = (x - μ)σ
Solution :
z-score = (9.25 - 9)0.73
= 0.250.73
z-score = 0.3425
p-value from Z-Table :
From the table
P(x < x1) = 0.6331
P(x > x1) = 1 - P(x < x1)
= 1 - 0.6331
P(x > x1) = 0.3669
Z-score calculator, p-value from z-table, left tail, right tail, two tail, formulas, work with steps, step by step calculation, real world and practice problems to learn how to find standard score for any raw value of X in the normal distribution. It also shows how to calculate the p-value from the z-table to find the probability of X in the normal distribution. It's an online statistics and probability tool requires an unstandardized raw value, mean of normal distribution, and the standard deviation. The result will describe the measure of how many number of standard deviations between a value and the mean. It is necessary to follow the next steps:
- Enter an unstandardized raw value, mean of normal distribution, and the standard deviation of the population in the box. These values must be real numbers and may be separated by commas. The values can be copied from a text document or a spreadsheet.
- Press the "GENERATE WORK" button to make the computation.
- z-score calculator will give the standard score for a data point.
Output : A real number or a variable.
z-score Formula:
z-score of a population data is determined by the formula $$z=\frac{x-\mu}{\sigma}$$ where $x$ is a random member, $\mu$ is an expected mean of population and $\sigma$ is the standard deviation of an entire population.
z-score Formula for Sample Data :
z-score of a sample data is determined by the formula $$z=\frac{x-\bar X}{s_X}$$ where $x$ is each value in the data set, $\bar{X}$ is the sample mean and $s_X$ is the sample standard deviation.
What is Z-score?
In statistics and probability, it is also called standard score, z-value, standardized score or normal score. A z-score measures the distance between an observation and the mean, measured in units of standard deviation. In other words, z-score is the number of standard deviations there are between a given value and the mean of the data set.
If a z-score is zero, then the data point's score is identical to the mean. If a z-score is 1, then it represents a value that is one standard deviation from the mean. Z-score may be positive or negative. A positive value represents the score above the mean (right tail) and a negative score represents the score below the mean (left tail). It is used to describe the normal distribution.
The standard normal distribution is the normal distribution with mean $0$ and standard deviation $1$. It is denoted as $N(0,1)$.
A random variable with the standard normal distribution is called a standard normal variable. Specific values of a standard normal variable are called z-values.
If $X$ is a normally distributed random variable with mean $\mu$ and standard deviation $\sigma$, then the distribution of $$Z =\frac{X-\mu}{\sigma}$$ is the standard normal distribution.
For a specific value $x$ of $X$, $\frac{x-\mu}{\sigma}$ is called the z-value. The z-value is a specific value of $Z$.
How to Calculate Z-Score?
To calculate a z-score, divide the deviation by the standard deviation, i.e.
$$z=\frac{\mbox{Deviation}}{\mbox{Standard Deviation}}$$
Since the deviation is the observed value of the variable, subtracted by the mean value, then the z-score is determined by the formula

In the following, we will give a stepwise guide for calculation the z-score for the given population.
- Find the mean of the population;
- Find the standard deviation of the population;
- Chose a random sample from the population;
- Find the difference between the value of random variable and population mean;
- Find the ratio between the difference and population standard deviation.
The class of five students scored $68, 75, 81, 87,$ and $90$. Find the normalized or z-score of $75$.
Following the previously exposed steps, we obtain
- $\mu =\frac{68 + 75 + 81 + 87 + 90}{5}= 80.2$
- $\sigma=\sqrt{\frac{(68 - 80.2)^2 + ( 75 - 80.2)^2 + ( 81 - 80.2)^2 + ( 87 - 80.2)^2 + ( 90 - 80.2)^2)}{5}}= 7.98498$
- By selecting $75$ as a random member from the population of $68, 75, 81, 87$, and $90$;
- The difference between the value of random variable and population mean is
$$75 - 80.2= -5.2$$
- The ratio between the difference and population standard deviation is
$$z-\mbox{score} =\frac{x -\mu}{\sigma}= \frac{-5.2}{7.98}= -0.6516$$
The z-score calculator, p-value calculation, z-table, formulas, solved example with step by step calculation to find the normalized, standard or relative standing value of a random variable of the normal distribution, calculated from the population of $68, 75, 81, 87$ and $90$. For any other values of random member, mean and standard deviation, just supply three real numbers and click on the "GENERATE WORK" button. The grade school students may use this Z-score calculator to generate the work, verify the results derived by hand or do their homework problems efficiently.
Z-Table
The Z-table helps to find the p-value of random variable in the normal distribution. The standard normal distribution is the normal distribution with mean 0 and standard deviation 1. It is denoted as $N(0,1)$. In this case, the probability density function is $$f(x)=\frac1{\sqrt{2\pi}} e^{-\frac{x^2}{2 }}$$
Because the standard normal distribution is used very often, there exist tables to help us calculate probabilities (Standard Normal Table).
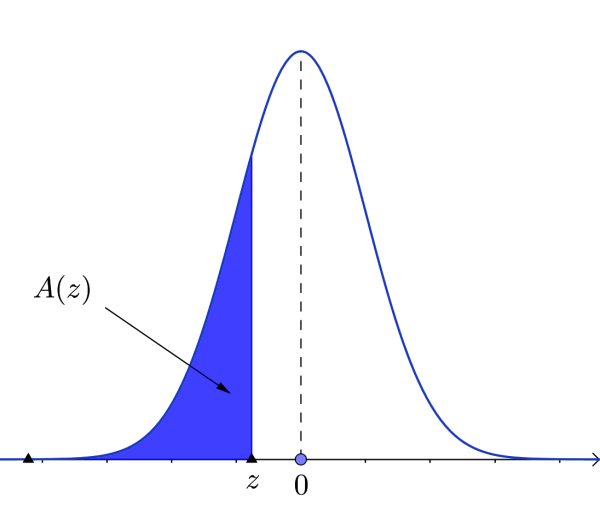
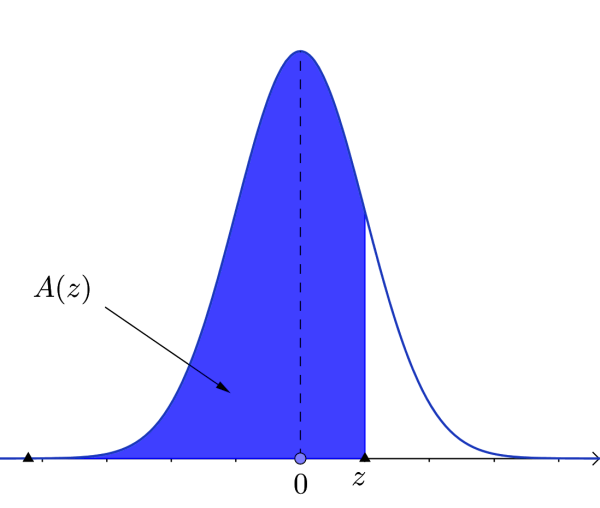
$A(z)$ is the integral of the standardized normal distribution from $-\infty$ to $z$, i.e. it represents the area under the standard normal curve from $0$ to the specified value of $z$.
| z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| -3.4 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0002 |
| -3.3 | 0.0005 | 0.0005 | 0.0005 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0003 |
| -3.2 | 0.0007 | 0.0007 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.0005 | 0.0005 | 0.0005 |
| -3.1 | 0.0010 | 0.0009 | 0.0009 | 0.0009 | 0.0008 | 0.0008 | 0.0008 | 0.0008 | 0.0007 | 0.0007 |
| -3.0 | 0.0013 | 0.0013 | 0.0013 | 0.0012 | 0.0012 | 0.0011 | 0.0011 | 0.0011 | 0.0010 | 0.0010 |
| -2.9 | 0.0019 | 0.0018 | 0.0018 | 0.0017 | 0.0016 | 0.0016 | 0.0015 | 0.0015 | 0.0014 | 0.0014 |
| -2.8 | 0.0026 | 0.0025 | 0.0024 | 0.0023 | 0.0023 | 0.0022 | 0.0021 | 0.0021 | 0.0020 | 0.0019 |
| -2.7 | 0.0035 | 0.0034 | 0.0033 | 0.0032 | 0.0031 | 0.0030 | 0.0029 | 0.0028 | 0.0027 | 0.0026 |
| -2.6 | 0.0047 | 0.0045 | 0.0044 | 0.0043 | 0.0041 | 0.0040 | 0.0039 | 0.0038 | 0.0037 | 0.0036 |
| -2.5 | 0.0062 | 0.0060 | 0.0059 | 0.0057 | 0.0055 | 0.0054 | 0.0052 | 0.0051 | 0.0049 | 0.0048 |
| -2.4 | 0.0082 | 0.0080 | 0.0078 | 0.0075 | 0.0073 | 0.0071 | 0.0069 | 0.0068 | 0.0066 | 0.0064 |
| -2.3 | 0.0107 | 0.0104 | 0.0102 | 0.0099 | 0.0096 | 0.0094 | 0.0091 | 0.0089 | 0.0087 | 0.0084 |
| -2.2 | 0.0139 | 0.0136 | 0.0132 | 0.0129 | 0.0125 | 0.0122 | 0.0119 | 0.0116 | 0.0113 | 0.0110 |
| -2.1 | 0.0179 | 0.0174 | 0.0170 | 0.0166 | 0.0162 | 0.0158 | 0.0154 | 0.0150 | 0.0146 | 0.0143 |
| -2.0 | 0.0228 | 0.0222 | 0.0217 | 0.0212 | 0.0207 | 0.0202 | 0.0197 | 0.0192 | 0.0188 | 0.0183 |
| -1.9 | 0.0287 | 0.0281 | 0.0274 | 0.0268 | 0.0262 | 0.0256 | 0.0250 | 0.0244 | 0.0239 | 0.0233 |
| -1.8 | 0.0359 | 0.0351 | 0.0344 | 0.0336 | 0.0329 | 0.0322 | 0.0314 | 0.0307 | 0.0301 | 0.0294 |
| -1.7 | 0.0446 | 0.0436 | 0.0427 | 0.0418 | 0.0409 | 0.0401 | 0.0392 | 0.0384 | 0.0375 | 0.0367 |
| -1.6 | 0.0548 | 0.0537 | 0.0526 | 0.0516 | 0.0505 | 0.0495 | 0.0485 | 0.0475 | 0.0465 | 0.0455 |
| -1.5 | 0.0668 | 0.0655 | 0.0643 | 0.0630 | 0.0618 | 0.0606 | 0.0594 | 0.0582 | 0.0571 | 0.0559 |
| -1.4 | 0.0808 | 0.0793 | 0.0778 | 0.0764 | 0.0749 | 0.0735 | 0.0721 | 0.0708 | 0.0694 | 0.0681 |
| -1.3 | 0.0968 | 0.0951 | 0.0934 | 0.0918 | 0.0901 | 0.0885 | 0.0869 | 0.0853 | 0.0838 | 0.0823 |
| -1.2 | 0.1151 | 0.1131 | 0.1112 | 0.1093 | 0.1075 | 0.1056 | 0.1038 | 0.1020 | 0.1003 | 0.0985 |
| -1.1 | 0.1357 | 0.1335 | 0.1314 | 0.1292 | 0.1271 | 0.1251 | 0.1230 | 0.1210 | 0.1190 | 0.1170 |
| -1.0 | 0.1587 | 0.1562 | 0.1539 | 0.1515 | 0.1492 | 0.1469 | 0.1446 | 0.1423 | 0.1401 | 0.1379 |
| -0.9 | 0.1841 | 0.1814 | 0.1788 | 0.1762 | 0.1736 | 0.1711 | 0.1685 | 0.1660 | 0.1635 | 0.1611 |
| -0.8 | 0.2119 | 0.2090 | 0.2061 | 0.2033 | 0.2005 | 0.1977 | 0.1949 | 0.1922 | 0.1894 | 0.1867 |
| -0.7 | 0.2420 | 0.2389 | 0.2358 | 0.2327 | 0.2296 | 0.2266 | 0.2236 | 0.2206 | 0.2177 | 0.2148 |
| -0.6 | 0.2743 | 0.2709 | 0.2676 | 0.2643 | 0.2611 | 0.2578 | 0.2546 | 0.2514 | 0.2483 | 0.2451 |
| -0.5 | 0.3085 | 0.3050 | 0.3015 | 0.2981 | 0.2946 | 0.2912 | 0.2877 | 0.2843 | 0.2810 | 0.3121 |
| -0.4 | 0.3446 | 0.3409 | 0.3372 | 0.3336 | 0.3300 | 0.3264 | 0.3228 | 0.3192 | 0.3156 | 0.2776 |
| -0.3 | 0.3821 | 0.3783 | 0.3745 | 0.3707 | 0.3669 | 0.3632 | 0.3594 | 0.3557 | 0.3520 | 0.3483 |
| -0.2 | 0.4207 | 0.4168 | 0.4129 | 0.4090 | 0.4052 | 0.4013 | 0.3974 | 0.3936 | 0.3897 | 0.3859 |
| -0.1 | 0.4602 | 0.4562 | 0.4522 | 0.4483 | 0.4443 | 0.4404 | 0.4364 | 0.4325 | 0.4286 | 0.4247 |
| -0.0 | 0.5000 | 0.4960 | 0.4920 | 0.4880 | 0.4840 | 0.4801 | 0.4761 | 0.4721 | 0.4681 | 0.4641 |
| z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9279 | 0.9292 | 0.9306 | 0.9319 |
| 1.5 | 0.9332 | 0.9345 | 0.9357 | 0.9370 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.9429 | 0.9441 |
| 1.6 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
| 1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
| 2.0 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.9920 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5 | 0.9938 | 0.9940 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.9970 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9981 |
| 2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3.0 | 0.9987 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |
| 3.1 | 0.9990 | 0.9991 | 0.9991 | 0.9991 | 0.9992 | 0.9992 | 0.9992 | 0.9992 | 0.9993 | 0.9993 |
| 3.2 | 0.9993 | 0.9993 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9995 | 0.9995 | 0.9995 |
| 3.3 | 0.9995 | 0.9995 | 0.9995 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 |
| 3.4 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9998 |
How to Find p-value from Z-Table
By using the Z-Table we can find probabilities for a statistical sample with a standard normal distribution. To find the p-value from the z-table we need to follow the next steps:
- Find the row which represents the ones digit and the tenths digit of the z-value;
- Find the column that represents the the hundredths digit of the z-value;
- Intersect the row and column from Steps 1 and 2;
For example, let us find the p-value for $P(Z < 1.13)$. Using the Z-Table, find the row for $1.1$ and the column for $0.03$.
Cumulative Standardized Normal Distribution
| z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
The intersection is 0.8708. Therefore, $P(Z < 1.13)=0.8708$.
As we mentioned, the total area under the normal curve is $1$. This means,
Cumulative Standardized Normal Distribution
| z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| -1.2 | 0.1151 | 0.1131 | 0.1112 | 0.1093 | 0.1075 | 0.1056 | 0.1038 | 0.1020 | 0.1003 | 0.0985 |
| -1.1 | 0.1357 | 0.1335 | 0.1314 | 0.1292 | 0.1271 | 0.1251 | 0.1230 | 0.1210 | 0.1190 | 0.1170 |
| -1.0 | 0.1587 | 0.1562 | 0.1539 | 0.1515 | 0.1492 | 0.1469 | 0.1446 | 0.1423 | 0.1401 | 0.1379 |
| -0.9 | 0.1841 | 0.1814 | 0.1788 | 0.1762 | 0.1736 | 0.1711 | 0.1685 | 0.1660 | 0.1635 | 0.1611 |
| -0.8 | 0.2119 | 0.2090 | 0.2061 | 0.2033 | 0.2005 | 0.1977 | 0.1949 | 0.1922 | 0.1894 | 0.1867 |
The intersection is 0.1292. We can conclude that
- $ P(Z\leq z)=\left\{ \begin{array}{ll} A(z), & z>0\ 1-A(z), & z<0 \end{array} \right. $
-
$ P(Z\geq z)=\left\{ \begin{array}{ll} 1-A(z), & z>0\ A(z), & z<0 \end{array} \right. $
-
$ P( z_1\leq Z\leq z_2)=A(z_2)-A(z_1)$
Real World Problems Using Z-score
The standard score transformation is useful to compare the relative standings between the members of the distribution with population mean and standard deviation. In other words, z-score determines how many standard deviations $\sigma$ a raw score of a random variable of the population above or below the population mean. Standard score is an important factor in statistics and probability to identify which random member in the normal distribution performing good, bad or moderate.
The graph of a standard normal distribution is called the standard normal curve. z-scores can be used to calculate probability (p-value) by comparing the location of the z-score to the area under a normal curve either to the left or right. A standard normal distribution has the following properties:
- The normal curve is bell shaped and is symmetric about the mean;
- The total area under the normal curve is equal to one.
Z-score Practice Problems
Practice Problem 1:
Find the z-score of a value of 35, if a mean of data set is 25, and a standard deviation is z.
Practice Problem 2:
Find the z-score of the price of a ball that cost $\$27$, if the mean ball price is $\$25.2$, with a standard deviation of 1.6.
Practice Problem 3:
Given a normal distribution with a mean of 237 and standard deviation of 56, find a value with a z-score of 1.94.
Practice Problem 4:
In a population that is normally distributed with mean 7 and standard deviation 11, the bottom 90% of the values are those less than x. Find the value of x.
Practice Problem 5:
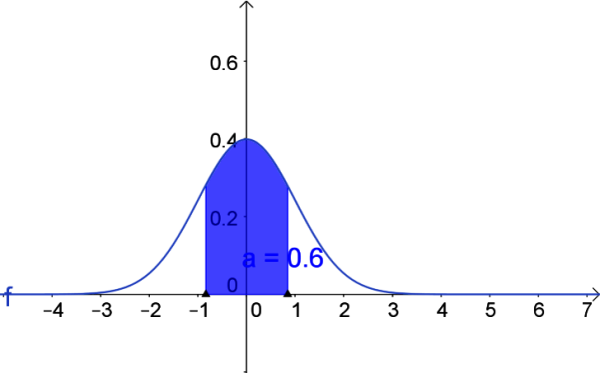
Find z-values correspond to the middle 60% of the standard normal distribution.